进阶5：状态变量型有源滤波器

状态变量型有源滤波器

目标

1. 了解状态变量型有源滤波器的电路原理

2. 学会利用集成运放搭建状态变量型有源滤波器

3. 学习利用ADALM2000分析滤波器的波特图

仪器仪表

仪器	元器件	工具
ADALM2000	10kΩ 电阻(1/4W)×7	面包板
	51kΩ 电阻(1/4 W)x3	导线
	1000pF 电容×2
	LM741 集成运放×4

仿真工具

Circuit JS

理论

利用比例、积分、求和等模拟运算来构成滤波器的传递函数，可以同时实现高通、低通、带通和带阻滤波功能，这种电路称为状态变量型有源滤波器，又称为多功能有源滤波器。 以高通滤波器为例，其传递函数为

$\frac{V_0(s)}{V_1(s)} = \frac{a_2 s^2}{s^2 + \frac{\omega_n}{Q}s + \omega_n^2}$

交叉相乘并移项，可得

$V_0(s) = a_2 V_i(s) - \frac{\omega_n}{Q} \frac{1}{s} V_o(s) - \omega_n^2 \frac{1}{s^2} V_o(s)$

表明Vo(s)为三项之和，即第一项为输入信号的a2倍，第二项为输出信号的一次积分，第三项为输出信号的二次积分。

这样，通过两个积分器和一个加法器就可以得到Vo(s)，如图1(a)所示。图1(b)是图1(a)的电路实现。

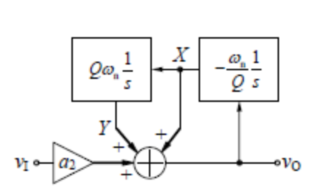(a) 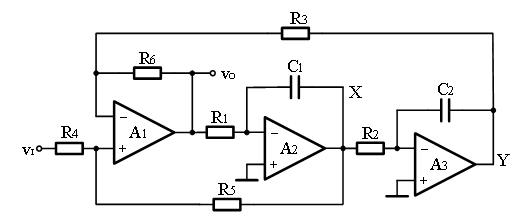（b）

图1：状态变量型二阶有源滤波器的电路实现

可以看出，图1(a)的Vo(s)实现了高通滤波功能，同时，Vo(s)的一次积分输出端X，即

$\frac{V_x(s)}{V_i(s)}=\frac{V_x(s)}{V_o(s)}\frac{V_o(s)}{V_i(s)}=\left(-\frac{\omega_n}{Q}\frac{1}{s}\right)\frac{a_2s^2}{s^2+\frac{\omega_n}{Q}s+\omega_n^2}=\frac{a_1s}{s^2+\frac{\omega_n}{Q}s+\omega_n^2}$

式中$a_{1} = -\frac{\omega_{n}}{Q} a_{2}$。实现了带通滤波器的传递函数。

类似的，Vo(s)的二次积分输出端Y，即

$\frac{V_y(s)}{V_i(s)}=\frac{V_y(s)}{V_x(s)}\frac{V_x(s)}{V_i(s)}=\left(\frac{Q\omega_n}{s}\right)\frac{a_1s}{s^2+\frac{\omega_n}{Q}s+\omega_n^2}=\frac{a_0}{s^2+\frac{\omega_n}{Q}s+\omega_n^2}$

式中$a_0 = Q\omega_n a_1$。实现了低通滤波器的传递函数。

可见，图1所示电路的三个不同输出端分别实现了高通、带通和低通。

UAF42集成电路就是利用这个原理实现的一种集成状态变量型有源滤波器，它可以接成同相或反相输入型。其内部框图如图2所示。

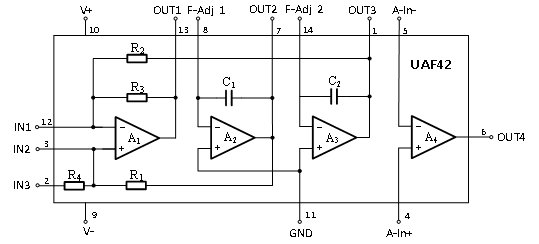图2：UAF42的内部框图

图3是UAF42的一种典型的应用电路，四个集成运放的输出Vo1、Vo2、Vo3、Vo4 分别实现高通、带通、低通和带阻滤波功能。

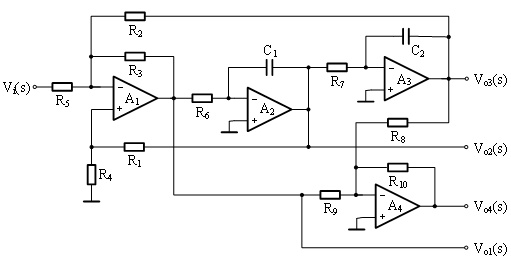图3:UAF42的一种典型应用电路

Circuit JS仿真

仿真实验电路:

图4:仿真实验电路

实验

1.按照图3，在面包板上搭建电路（R1 = R2 = R3 = 51kΩ，R4 ~ R10 =10kΩ，C1 = C2 = 1000pF，集成运放为LM741）。

参考图:

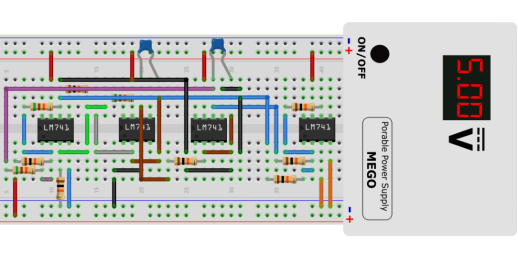图5:实验电路

2.利用ADALM2000的网络分析仪，测试四种滤波器的波特图。

高通：

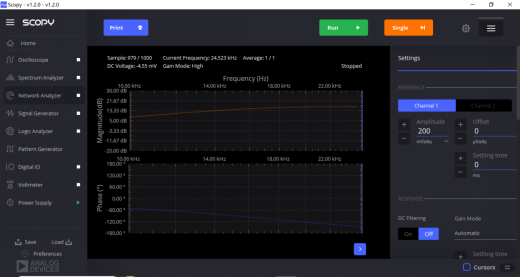图6:高通波特图

带通：

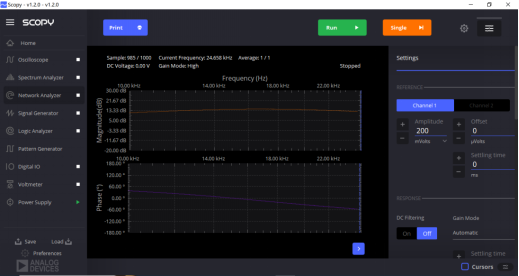图7:带通波特图

低通：

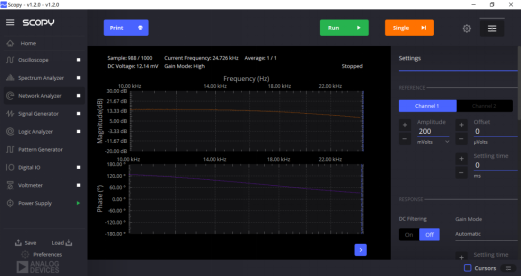图8:低通波特图

带阻：

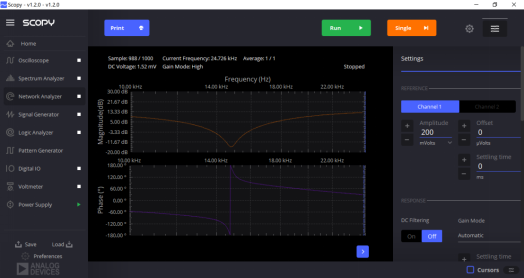图9:带阻波特图

练习

利用UAF42，设计一个数控有源滤器。

参考图：

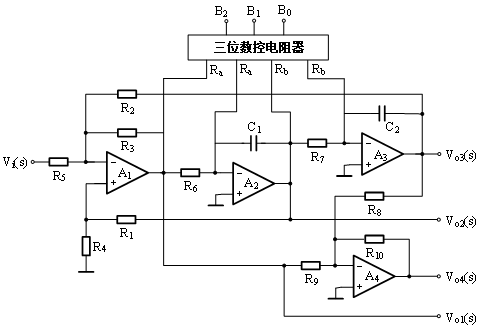图10：数控有源滤波器 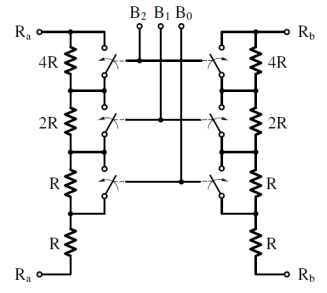图11：数控变阻器

Circuit JS仿真：

图12：数控有源滤波器仿真图