实验9：RC电路

一阶RC电路

目标

1．学习使用示波器观察一阶RC电路响应

2．掌握测定一阶RC电路时间常数的方法

仪器仪表

仪器	元器件	工具
梅林雀	- 300Ω 电阻(1/4w)×1	- 面包板
	- 1μF 电容×1	- 导线

仿真工具

Circuit JS

理论

1.RC电路的矩形脉冲响应

如图1所示，将矩形脉冲序列信号作用于电压初值为零的RC串联电路上，图中矩形脉冲的脉宽tp= 0.5mS，RC电路的时间常数τ = 0.1mS，满足tp >> τ的条件(经验值为tp大于(4 ~ 5)τ即可)，则可近似认为矩形脉冲电平每次改变后，电容C都能够充分地完成充放电，电路中电阻R和电容C上的电压波形如图2所示。

图1：RC串联电路

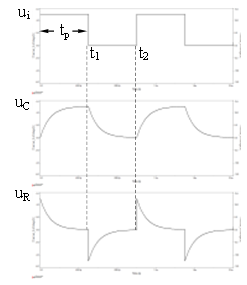图2：RC电路的矩形脉冲响应

若矩形脉冲的幅度为E，脉宽为tp，则电容上的电压可表示为：

u_c(t) = \begin{cases} E\left(1 - e^{-\frac{t}{\tau}}\right), & 0 \leq t \leq t_1 \\ Ee^{-\frac{t}{\tau}}, & t_1 < t \leq t_2 \end{cases}

电阻上的电压可表示为：

u_R(t) = \begin{cases} Ee^{-\frac{t}{\tau}}, & 0 \leq t \leq t_1 \\ -Ee^{-\frac{t}{\tau}}, & t_1 < t \leq t_2 \end{cases}

即当0到t1时，电容经电阻R充电；当t1到t2时，电容器经电阻R放电。由于电容两端电压不能突变，而电流可以突变，所以图中电阻两端的电压发生了突变。

2.时间常数τ的测量方法

如图3所示，利用方波来模拟阶跃激励信号，即方波的上升沿作为零状态响应的正阶跃激励信号；方波的下降沿作为零输入响应的负阶跃激励信号。注意选择方波的重复周期远大于电路的时间常数，得到的响应如图4所示。

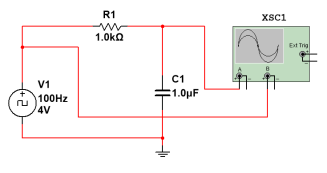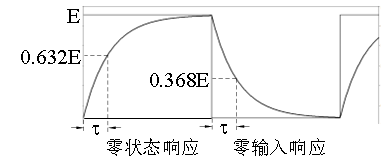图3：利用方波来模拟阶跃激励信号 alt text

图4：RC电路及其响应

根据零状态响应，有

u_c(t)=E\left(1-e^{-\frac{t}{\tau}}\right)

当t = τ时，uc (t) = 0.632E，即与此电压对应的时间就等于时间常数，如图4所示。类似地，根据零输入响应，有

这张图片展示了一个数学公式，具体为：

u_c(t)=Ee^{-\frac{t}{\tau}}

当t = τ时，uc (t) = 0.368E，即与此电压对应的时间也等于时间常数，如图4所示。

Circuit JS仿真

图5：RC串联仿真电路

分别选中V1，C1，R1右击选择在新示波器中查看，可以看到下图仿真波形。

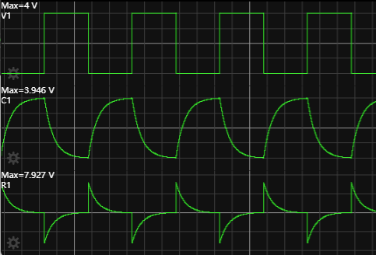图6：RC电路的矩形脉冲响应

实验

按照图3电路，在面包板上搭建电路，选择R = 300Ω，C = 1μF，输入方波信号，可由梅林雀产生，其方波参数为1Vpp，偏置0.5V，占空比50%，频率100Hz。用梅林雀示波器两个通道，同时观测输入、输出波形，并记录。

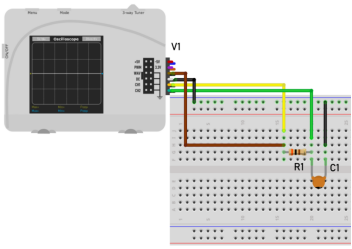图7：利用方波来模拟阶跃激励信号实物电路

测量该RC电路时间常数τ，并与理论值比较。

表格1

输入波形	输出波形

表格2

τ测量值	τ理论值

练习

电路如图8所示，取RC电路的电容两端作为输出端，使电路参数满足τ >>tp的条件，则为积分电路。由于此时电容器充放电进行得很慢，因此电阻R上的电压uR(t)近似等于输入电压ui(t)，这时输出电压uo(t)即C的端电压为：

u_o(t)=u_c(t)=\frac{1}{C}\int i_c(t)\mathrm{d}t=\frac{1}{C}\int\frac{u_R(t)}{R}\mathrm{d}t\approx\frac{1}{RC}\int u_i(t)\mathrm{d}t

表明输出电压uo(t)与输入电压ui(t)近似为积分关系。

图8：RC积分电路

积分电路的输入输出波形如图9所示。

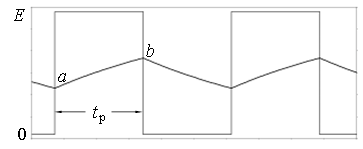图9：积分电路的输入输出波形

通过求解电路，可以得到

\tau=\frac{t_{p}}{\ln\frac{u_{b}}{u_{a}}}

式中ua和ub分别为电容电压的最小值和最大值。利用示波器测得tp、ua和ub的值，即可间接得到电路的时间常数。或者表示为

\tau=\frac{t_{p}}{\ln\frac{E+\Delta u}{E-\Delta u}}

式中 $\Delta \mathrm{u} = \mathrm{u}_\mathrm{b} - \mathrm{u}_\mathrm{a}$ 为三角波的峰峰值。利用示波器测得E、tp和 $\Delta$ u的值，也可间接得到电路的时间常数。当三角波ab段近似为直线时，可求得

\tau \approx\frac{Et_p}{2\Delta u}

即利用示波器测得E、tp和 $\Delta$ u的值，可间接得到电路的时间常数。

Circuit JS仿真：

图10：RC积分仿真电路

一阶RC电路​

一阶RC电路