实验3：惠斯通电桥

目标

1.熟悉惠斯通电桥的结构及其搭建

2.学会惠斯通电桥平衡的调节

3.通过惠斯通电桥实验确定未知电阻的阻值

仪器仪表

仿真工具

Circuit JS

理论

惠斯通电桥通常有四个电阻组成，如图所示，其中三个电阻为已知电阻，另一个电阻为待测电阻，其阻值可通过已知电阻求得。在下图电路中，R1，R2，R3为已知电阻，Rx为待测电阻。

图1:惠斯通电桥电路图

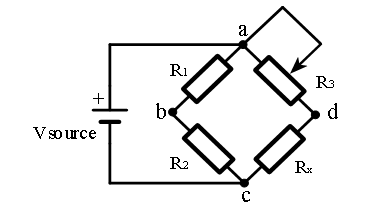
在电路中，电压Vbc由R1，R2组成的分压电路决定，电压Vdc由R3，Rx组成的分压电路决定。调节R3阻值，当Vbc = Vdc时，就构成了一个平衡的惠斯通电桥。利用惠斯通电桥的平衡条件，可以得出:

\frac{R_{1}}{R_{2}} = \frac{R_{3}}{R_{x}}

由此可以求得Rx。

当惠斯通电桥不平衡时，则有Vbc > Vdc或者Vbc < Vdc，据此，利用惠斯通电桥可以使电压Vbd为零、正或负电压。所以，在实际电子产品中，惠斯通电桥的应用非常广泛，常被应用于各种压力，应力，形变测量和温度传感器中。

Circuit JS 仿真

在Circuit JS仿真界面搭建惠斯通电路（Circuit JS使用步骤参考实验1），选择12V电压，选择一个电阻作为待测电阻Rx，假设为2.2kΩ，R1=1.2kΩ，R2=1kΩ，R3为可变电阻。通过调节R3，使惠斯通电桥平衡，利用平衡条件，能够计算出Rx的值为2.2kΩ，假设成立。

图2:惠斯通电桥电路仿真

实验

1.参考图1，在面包板上构建惠斯通电桥电路。其中，V~~source~~ = 6V，Rx = 2.2kΩ，R1 = 1.2kΩ，R2 = 1.0kΩ，R3为5.1kΩ可变电阻。按图3方法连接。

图3:面包板电路图

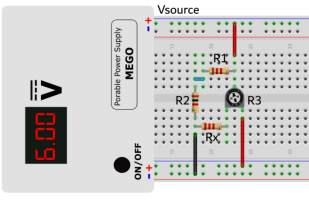
2.使用万用表测量R1，R2和Rx的阻值，并记录在表1中。

如图2所示，测量b和d之间的压降。并调节可变电阻R3，使b和d之间的压降接近0V，以达到平衡状态。

图4:测量Vbd

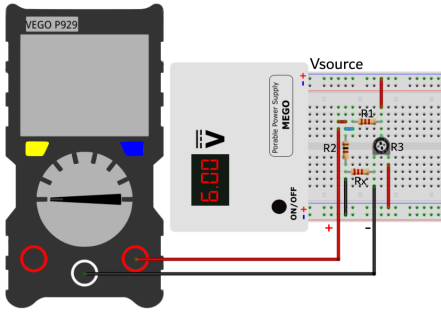
3.关闭MEGO并断开可变电阻，使用万用表测量R3。注意，可变电阻有3个引脚，只有接入电路的其中2个引脚是需要被测量的阻值。测量结果记录在表1中。

表1:测量阻值

R1	R2	R3	Rx

实验结果：用R1，R2和R3推导出Rx的值，并与Rx的标称值和万用表测量值比较。

练习

设计一个电阻-电压转换器，要求：电路采用单电源供电，当电阻R在(0.8 ~ 1.2kΩ)之间变化时，输出电压V0在(-1.1 ~ 0.9V)之间变化。

参考答案：

图5:电阻-电压转换器电路

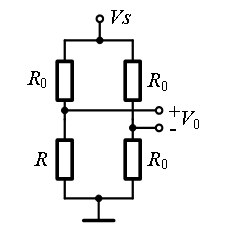
电路如图所示，根据电阻R变化范围，可知桥式电路中其余三个电阻R0的取值应为0.8 ~ 1.2kΩ的中间值，即1kΩ。

根据图5电路，可知：

1.当R = 0.8kΩ时，V0 = -1.1V，于是有

-1.1 = \left(\frac{0.8}{1 + 0.8} - \frac{1}{1 + 1}\right) V_s

2.当R = 1.2kΩ时，V0 = 0.9V，于是有

0.9 = \left(\frac{1.2}{1 + 1.2} - \frac{1}{1 + 1}\right) V_s

据此推出VS = 19.8V，取20V。

Circuit JS仿真：

图6：当R = 0.8kΩ时，V0 = -1.1V 图7：当R = 1.2kΩ时，V0 = 0.9V