实验10：电感器

电感器

目标

1. 使用数字万用表测量电感器的参数

2. 计算RL电路的时间常数τ

3. 在充满电的条件下观察电感器的特性

仪器仪表

仪器	元器件	工具
直流电压源	- 1.0kΩ 电阻(1/4W)×1	- 面包板
数字万用表	- 10mH 电感(1W)×1	- 导线
梅林雀

仿真工具

Circuit JS

理论

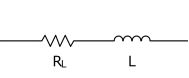
电感器与电容器类似，都是可以储存能量的电子元件。电容器是以电场的形式存储能量，而电感器则是以磁场形式存储能量。电感的度量单位是亨利，用H表示。与电容相比，理想的电感在满负荷时可视为短路 (相当于一根导线)，在现实中，非理想的电感器可以看成一个理想电感与一个内部电阻RL的串联结构，如图1所示。

图1：非理想的电感器

与RC电路相同，在RL组成的串联电路中，电感电流达到其满载值所需的时间也约等于5倍的时间常数(5τ)，在RL电路，时间常数的计算方法如下:

$\tau =\frac{L}{R}$

其中R的单位是欧姆，L的单位亨利。

对于理想的电感，其满载时的直流端电压为0V，而对于非理想电感，由于其内阻不为零，因此电感两端会存在很小的压降。注意，电感的内阻不是实际存在于器件，而是所展现出的一种等效电阻的物理特性，所以需要和实际的电阻器加以区分。

在串联与并联电路中，等效电感的计算方法如下: 电感串联：

$L_{total}=L_1+L_2+L_3+\ldots$

电感并联：

$\frac{1}{L_{total}}=\frac{1}{L_1}+\frac{1}{L_2}+\frac{1}{L_3}+\ldots$

Circuit JS仿真

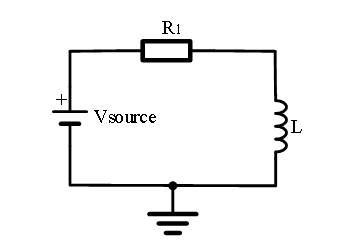
RL串联电路：其中，Vsource = 9 V，R1 = 1kΩ，L = 10 mH。

图2：理想的R-L电路

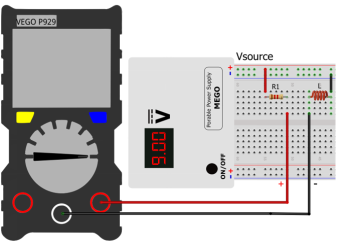
使用VEGO测量电感中的电流IL-measured。

图3: 测量L的端电压

使用VEGO测量电感两端的电压VL-measured。

图4：测量流过L的电流

实验

一．计算理想电感的时间常数

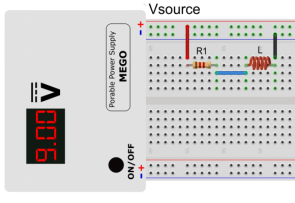
1.搭建图5的RL串联电路。其中，Vsource = 9V，R1 = 1kΩ，L = 10mH。面包板电路可参考图6。测量R1并将测量值填入表1的第1列。

图5:理想的R-L电路 图6: R-L面包板电路

2.使用以下公式计算时间常数τ。将计算值填入表1的第2列。

$\tau =\frac{L}{R}$

3.由于电感在满载后如同短路，这就意味着VL的压降为0，见表1第3列。现在使用欧姆定律来计算电感器的满载电流，将计算结果IL-calculated记录在表1第4列。

二．测量非理想的电感器 1.为确保电感已达到满载，在打开MEGO电源后等待一段时间，并确保该时间至少大于5τ。

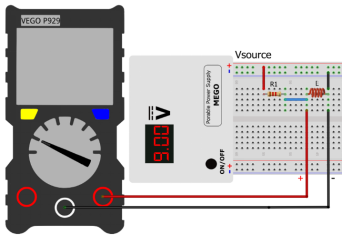
2.现在使用VEGO测量电感中的电流IL-measured以及电感两端的电压VL-measured。测量方式可以参考图7和图8。测量结果列入表1的第5列和第6列。

图7: 测量L的端电压 图8：测量流过L的电流 表1

R1-measured	τ	VL-calculated	IL-calculated	IL-measured	VL-measured
		0 V

3.在表1中，如果发现VL-measured值不为0V，且IL-measured的值与IL-calculated的计算值偏差较大，则是由于电感器的内阻RL导致的。图9给出了更真实的电感模型。

图9：电感内部的等效电路

4.我们可以通过两种方法确定电感器的内阻(RL)。第一种方法是将VEGO调成欧姆表后直接测量电感器。将测量值记录在表2的第1列。

5.第二种方法是使用欧姆定律来计算内阻。提示：在表1中我们测量了电感两端的压降以及流过它的电流。将计算出的电感内阻记录在表2第2列中。

表2

RL-measured	RL-calculated

练习

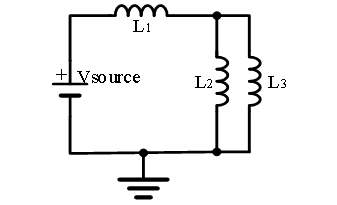
1.计算图10电路的总电感，并画出等效电路。其中，Vsource = 10 V，L1 = 100 mH，L2 = 220 mH，L3 = 10 mH。

图10

2.假设图11电路中的电感器是理想的。计算该电路中的时间常数，以及电感充满电的时间。提示:可以使用戴维南定理将该电路等效为一个电压源与电阻串联的结构。

图11

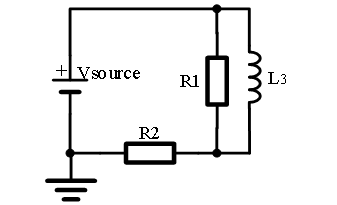
3.在题目2的电路中，假设电感器是非理想的，且内阻RL等于63Ω。该电路在满载后，R1和R2两端的压降分别是多少？

Circuit JS 仿真

图12 图13