1.4 电磁波

波在自然界中无处不在，能够将能量或信息从源头传递到目的地。波既是空间的函数，也是时间的函数。一种奇特的波是电磁波，它的存在由海因里希·赫兹教授证明，但麦克斯韦本人此前就预测了电磁波的存在。

这些波可以在真空中传播，不需要任何介质。它们与机械波（如声波）不同，机械波需要通过物质介质来传播其能量。

因此，与机械波不同，电磁波可以在真空中传播。典型的电磁波例子包括可见光波、无线电波、雷达波束和电视信号。电磁波是一种复合现象，涉及电场和磁场。

均匀平面波和波动方程

均匀平面波的基本概念为理解电磁波在介质中的传播提供了基础。均匀平面波是电磁学中的一个基本概念，它是麦克斯韦方程在无界、均匀介质中时变场的最简单解。

尽管在实际中不存在无界、均匀的介质，但均匀平面波的基本概念对于了解电磁波非常有用。此外，在许多实际问题中，均匀平面波的解相当有用且足够。

在某些情况下，当介质的物理尺寸远大于波长时，解可以近似为均匀平面波解。

考虑一个均匀的、各向同性的、无界的介质，其中不包含任何电或磁源。在这种情况下，介质的磁导率 $\mu$ 和介电常数 $\epsilon$ 在整个介质中是恒定的。由于介质是无源的，因此介质中没有自由电荷。麦克斯韦方程为：

$\nabla \cdot \overline{D} = 0$ $\nabla \cdot \overline{B} = 0$ $\nabla \times \overline{E} = - \frac{\partial \overline{B}}{\partial t}$ $\nabla \times \overline{H} = \overline{J} + \frac{\partial \overline{D}}{\partial t}$

从本构关系中，我们有：

$\overline{B} = \mu \overline{H}$ $\overline{D} = \epsilon \overline{E}$ $\overline{J} = \sigma \overline{E}$

由于介质是均匀的且不随时间变化，因此磁导率 $\mu$ 和介电常数 $\epsilon$ 是时间和空间的常数。因此，麦克斯韦方程变为：

$\nabla \cdot \overline{B} = \nabla \cdot (\mu \overline{H}) = \mu \nabla \cdot \overline{H} = 0$ $\nabla \cdot \overline{H} = 0 \quad \text{(1)}$ $\nabla \cdot \overline{D} = \nabla \cdot (\epsilon \overline{E}) = \epsilon \nabla \cdot \overline{E} = 0$ $\nabla \cdot \overline{E} = 0 \quad \text{(2)}$ $\nabla \times \overline{E} = - \frac{\partial (\mu \overline{H})}{\partial t}$ $\nabla \times \overline{E} = - \mu \frac{\partial \overline{H}}{\partial t} \quad \text{(3)}$ $\nabla \times \overline{H} = \frac{\partial (\epsilon \overline{E})}{\partial t}$ $\nabla \times \overline{H} = \sigma \overline{E} + \epsilon \frac{\partial \overline{E}}{\partial t} \quad \text{(4)}$

在上述方程中，$\nabla$ 表示对空间的微分，而 $\frac{\partial}{\partial t}$ 表示对时间的微分。从方程 (3) 和 (4) 可以看出，磁场的时间导数与电场的空间导数有关，同样，电场的时间导数与磁场的空间导数有关。

因此，从这两个方程可以看出，时变磁场不能独立于相应的电场和磁场存在。因此，电场和磁场必须共同存在才能产生时变场。

对于这种时变场，我们不能得到只有磁场或只有电场的时变场。但在电静学和磁静学这种时不变场的情况下，它们可以独立存在。

对方程 (3) 和 (4) 取旋度，我们得到：

$\nabla \times \nabla \times \overline{E} = - \mu \nabla \times \frac{\partial \overline{H}}{\partial t}$ $\nabla \times \nabla \times \overline{H} = \nabla \times (\sigma \overline{E}) + \nabla \left( \epsilon \frac{\partial \overline{E}}{\partial t} \right)$

由于 $\nabla$ 和 $\frac{\partial}{\partial t}$ 是相互独立的，因此可以交换操作符：

$\nabla \times \nabla \times \overline{E} = - \mu \frac{\partial (\nabla \times \overline{H})}{\partial t}$ $\nabla \times \nabla \times \overline{H} = \sigma (\nabla \times \overline{E}) + \epsilon \frac{\partial (\nabla \times \overline{E})}{\partial t}$

将方程 (3) 和 (4) 中的 $\nabla \times \overline{H}$ 和 $\nabla \times \overline{E}$ 的值代入，我们得到：

$\nabla \times \nabla \times \overline{E} = - \mu \frac{\partial}{\partial t} (\sigma \overline{E} + \epsilon \frac{\partial \overline{E}}{\partial t})$ $\nabla \times \nabla \times \overline{E} = - \mu \sigma \frac{\partial \overline{E}}{\partial t} - \mu \epsilon \frac{\partial^2 \overline{E}}{\partial t^2}$

同样地：

$\nabla \times \nabla \times \overline{H} = \sigma \left( - \mu \frac{\partial \overline{H}}{\partial t} \right) + \epsilon \frac{\partial}{\partial t} \left( - \mu \frac{\partial \overline{H}}{\partial t} \right)$ $\nabla \times \nabla \times \overline{H} = - \mu \sigma \frac{\partial \overline{H}}{\partial t} - \mu \epsilon \frac{\partial^2 \overline{H}}{\partial t^2}$

利用矢量恒等式 $\nabla \times \nabla \times \overline{A} = \nabla (\nabla \cdot \overline{A}) - \nabla^2 \overline{A}$，其中 $\overline{A}$ 是任意矢量，那么上述方程可以写为：

$\nabla (\nabla \cdot \overline{E}) - \nabla^2 \overline{E} = - \mu \frac{\partial}{\partial t} (\sigma \overline{E} + \epsilon \frac{\partial \overline{E}}{\partial t})$ $\nabla (\nabla \cdot \overline{H}) - \nabla^2 \overline{H} = - \mu \sigma \frac{\partial \overline{H}}{\partial t} - \mu \epsilon \frac{\partial^2 \overline{H}}{\partial t^2}$

根据方程 (1) 和 (2)，$\nabla \cdot \overline{E} = 0$ 和 $\nabla \cdot \overline{H} = 0$，因此：

$- \nabla^2 \overline{E} = - \mu \sigma \frac{\partial \overline{E}}{\partial t} - \mu \epsilon \frac{\partial^2 \overline{E}}{\partial t^2}$ $\nabla^2 \overline{E} = \mu \sigma \times \frac{\partial \overline{E}}{\partial t} + \mu \epsilon \left( \frac{\partial^2 \overline{E}}{\partial t^2} \right) \quad \text{(5)}$

这是介质中电场 $\overline{E}$ 的波动方程。同样地，

$-\nabla^2 \overline{H} = -\mu \sigma \left( \frac{\partial \overline{H}}{\partial t} \right) - \mu \epsilon \left( \frac{\partial^2 \overline{H}}{\partial t^2} \right)$ $\nabla^2 \overline{H} = \mu \sigma \left( \frac{\partial \overline{H}}{\partial t} \right) + \mu \epsilon \left( \frac{\partial^2 \overline{H}}{\partial t^2} \right) \quad \text{(6)}$

这是介质中场 $\overline{H}$ 的波动方程。

上述方程 (5) 和 (6) 是波动方程，它们的解表示了三维空间中的波动现象。最终，我们得出结论：在均匀的、无界的介质中，时变场的存在形式必须是波的形式。

此外，电场和磁场必须同时存在。这就是这种现象被称为电磁波的原因。

但对于自由空间，$J = 0$，$\sigma = 0$，$\epsilon = \epsilon_0$，$\mu = \mu_0$。将这些值代入方程 (5) 和 (6)，我们得到

$\nabla^2 \overline{E} = \mu_0 \epsilon_0 \left( \frac{\partial^2 \overline{E}}{\partial t^2} \right)$ $\nabla^2 \overline{H} = \mu_0 \epsilon_0 \left( \frac{\partial^2 \overline{H}}{\partial t^2} \right)$

电磁波沿 $Z$ 平面方向传播，因此向量 $\overline{E}$ 和 $\overline{H}$ 与 $x$ 和 $y$ 无关。因此，向量 $\overline{E}$ 和 $\overline{H}$ 是 $z$ 和 $t$ 的函数。因此，上述方程变为

$\frac{\partial^2 \overline{E}}{\partial z^2} = \mu_0 \epsilon_0 \left( \frac{\partial^2 \overline{E}}{\partial t^2} \right)$

通过重新排列项，我们得到

$\frac{\partial^2 \overline{E}}{\partial t^2} = \left( \frac{1}{\mu_0 \epsilon_0} \right) \left( \frac{\partial^2 \overline{E}}{\partial z^2} \right)$

根据物理学中的结果，

光速 $v = \left( \frac{1}{\sqrt{\mu_0 \epsilon_0}} \right) = 3 \times 10^8 \, \text{m/s}$

$v^2 = \left( \frac{1}{\mu \epsilon} \right)$

将上述值代入方程，我们得到

$\frac{\partial^2 \overline{E}}{\partial t^2} = v^2 \left( \frac{\partial^2 \overline{E}}{\partial z^2} \right)$

同样地

$\frac{\partial^2 \overline{H}}{\partial t^2} = v^2 \left( \frac{\partial^2 \overline{H}}{\partial z^2} \right)$

平面波传播

电磁波在介质中的特性由电参数（如磁导率、介电常数和电导率）决定。电磁波与电场和磁场相关，这两个场相互垂直，并且都垂直于传播方向。

通常，传播方向沿 $Z$ 轴。在自由空间中，所有电磁波的传播速度等于光速，即 $3 \times 10^8$ m/s。传播方向垂直于由磁场和电场向量形成的平面。

这些场的相位与 $x$ 和 $y$ 轴无关，因此在与传播方向正交的平面上不存在相位变化。

在特定方向的平面上，幅度和方向均匀的波被称为平面波。电磁波场（电场和磁场）的幅度在 $xy$ 平面上是恒定的，且恒定相位的表面与 $xy$ 平面平行，因此这些波被称为平面波。

根据麦克斯韦旋度方程，振荡的电场产生磁场通量，而磁场通量进一步振荡以产生电场。这两个场之间的相互作用导致能量的存储，从而携带功率。

波的重要特性是幅度、相位或频率，这些特性使得波能够从源端携带信息到目的端。

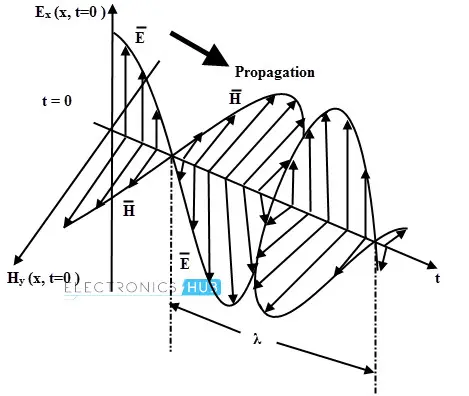
对于均匀平面波，其电场是 $x$ 和时间 $t$ 的函数，且与 $y$ 和 $z$ 轴无关。

这些波本质上是横向电磁波（TEM 波），其中 $E$ 和 $H$ 场始终具有恒定的幅度，并且在时间上是同相的。 $E$ 和 $H$ 场传输的功率沿传播方向。

电磁波极化

需要明确的是，均匀平面波的电场矢量方向随时间变化，这决定了波的极化方式。这是因为某些应用只能接收或发射一种类型的极化电磁波，最好的例子是射频应用中不同类型的天线被设计为接收或发射一种特定极化的波。

在平面电磁波中，电场在 $xz$ 平面内振荡，而磁场在 $yz$ 平面内振荡。因此，它对应于一种极化波。电场振荡所在的平面被定义为极化平面。

极化不过是电场随幅度和方向变化的一种方式。极化可以是线性极化、圆极化或椭圆极化。假设 $\overline{E}_x$ 和 $\overline{E}_y$ 分别是沿 $x$ 轴和 $y$ 轴方向的电场，而 $\overline{E}$ 是 $\overline{E}_x$ 和 $\overline{E}_y$ 的合成矢量。

线性极化

如果电磁波的电场平行于 $x$ 轴，则称该波为沿 $x$ 方向线性极化。平行于 $x$ 轴的直线天线可以产生这种极化波。类似地，沿 $y$ 轴方向也可以产生和定义 $y$ 极化波。

假设 $\overline{E}$ 同时具有 $\overline{E}_x$ 和 $\overline{E}_y$ 分量，且这两个分量同相但幅度不同。由于 $\overline{E}_x$ 和 $\overline{E}_y$ 同相，它们的幅度同时达到最大值和最小值。因此，在正 $z$ 轴上的任意一点，这两个分量的幅度比值是恒定的。

因此，合成电场 $\overline{E}$ 的方向取决于 $\overline{E}_x$ 和 $\overline{E}_y$ 的相对幅度。因此， $\overline{E}$ 与 $x$ 轴之间的夹角 $\theta$ 由下式给出：

$\theta = \tan^{-1} \left( \frac{E_y}{E_x} \right)$

其中 $E_y$ 和 $E_x$ 分别是 $\overline{E}_y$ 和 $\overline{E}_x$ 的幅度。

从时间上看，这个角度是恒定的，因此该波被称为线性极化。因此，当 $\overline{E}_x$ 和 $\overline{E}_y$ 同相（无论幅度是否相等）时，沿 $z$ 方向传播的均匀平面波的极化是线性的。

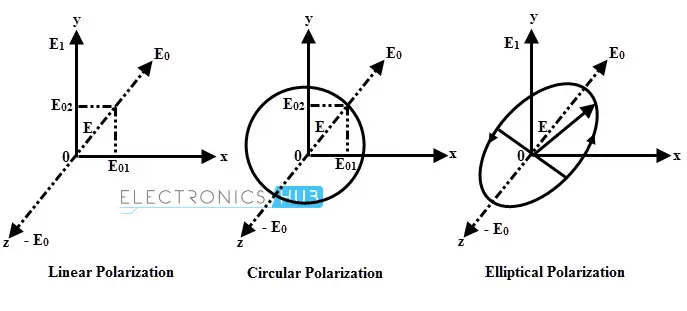
圆极化

如果两个正交极化的分量 $\overline{E}_y$ 和 $\overline{E}_x$ 幅度相等，但相位差为 90 度，则合成波为圆极化。在这种情况下，在任意时刻，如果其中一个分量的幅度达到最大值，那么另一个分量的幅度由于相位差而变为零。

也可以这样描述：如果其中一个分量的幅度逐渐增加，那么另一个分量的幅度则逐渐减小，反之亦然。因此，合成矢量 $\overline{E}$ 的幅度在任意时刻是恒定的，但方向是 $\overline{E}_y$ 和 $\overline{E}_x$ 相对幅度之间夹角的函数。

如果将合成电场 $\overline{E}$ 投影到垂直于传播方向的平面上，那么所有这些点的轨迹是一个以 $z$ 轴为中心的圆，如图所示。

在一个波长范围内，场矢量 $\overline{E}$ 旋转 360 度，或者换句话说，完成一个旋转周期，因此这种波被称为圆极化。

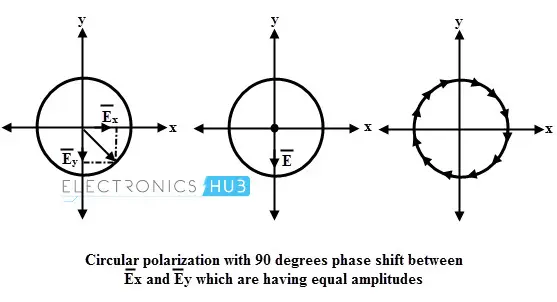
圆极化可以是右旋圆极化（RHCP）或左旋圆极化（LHCP）。RHCP 波描述的是在传播方向上看起来电场矢量顺时针旋转的波。

对于 LHCP 波，矢量场则逆时针旋转。因此，如果两个电场矢量分量的幅度相等，并且它们之间的相位差为 90 度，则均匀平面波的极化是圆极化的。

椭圆极化

在大多数情况下，波的分量具有不同的幅度，并且相位角不是 90 度。这导致了椭圆极化。假设电场具有 $\overline{E}_x$ 和 $\overline{E}_y$ 两个分量，它们的幅度不相等，且不同相。

当波传播时， $\overline{E}_x$ 和 $\overline{E}_y$ 的最大和最小幅度值不是同时出现的，而是出现在不同的时间点。因此，合成场矢量的方向随时间变化。

如果追踪场矢量 $\overline{E}$ 的端点轨迹，可以观察到 $\overline{E}$ 在平面上呈椭圆运动。因此，这种波被称为椭圆极化。

电磁波在不同介质中的传播

在电磁场中，材料被分类为导体、电介质和损耗电介质。电参数（如磁导率 $\mu$、介电常数 $\epsilon$ 和电导率 $\sigma$）是决定介质类型的可变参数。不同的材料对电磁波的影响各不相同。

例如，当我们穿过隧道或在桥下时，收音机可能会失去信号。此外，与白天相比，夜间收音机信号的接收效果通常更好。这表明电磁波会受到材料或环境条件的影响。

因此，了解电磁波的传播特性对于选择合适的频率、功率、波的类型以及其他设计应用（如传输线、天线、波导等）所需的参数至关重要。

考虑从方程 (5) 和 (6) 中得到的介质中的波：

$\nabla^2 \overline{E} = \mu \sigma \times \frac{\partial \overline{E}}{\partial t} + \mu \epsilon \left( \frac{\partial^2 \overline{E}}{\partial t^2} \right)$ $\nabla^2 \overline{H} = \mu \sigma \left( \frac{\partial \overline{H}}{\partial t} \right) + \mu \epsilon \left( \frac{\partial^2 \overline{H}}{\partial t^2} \right)$

对于均匀平面波，电场和磁场都随时间变化。因此，可以将时间的偏导数替换为 $j\omega$。于是，电场和磁场可以表示为：

$\nabla^2 \overline{E} = \mu \sigma \times (j\omega \overline{E}) + \mu \epsilon (j\omega)^2 \overline{E}$ $\nabla^2 \overline{E} = [j\omega \mu (\sigma + j\omega \epsilon)] \overline{E}$

同样地，

$\nabla^2 \overline{H} = [j\omega \mu (\sigma + j\omega \epsilon)] \overline{H}$

上述两个方程被称为波形中的波动方程。在这些方程中，括号内的项是相同的，它代表了电磁波传播的介质的特性。这个项等于传播常数 $\gamma$ 的平方。因此，波动方程变为：

$\nabla^2 \overline{E} = \gamma^2 \overline{E}$ $\nabla^2 \overline{H} = \gamma^2 \overline{H}$

以介质的特性表示，传播常数为：

$\gamma = \sqrt{j\omega \mu (\sigma + j\omega \epsilon)} = \alpha + j\beta$

一般来说，当电磁波通过介质传播时，会发生衰减，因此波的幅度也会衰减。这由传播常数的实部表示，即

$\alpha = \omega \sqrt{\left( \frac{\mu \epsilon}{2} \right) \sqrt{1 + \left( \frac{\sigma}{\omega \epsilon} \right)^2} - 1}$

同样地，当电磁波通过介质传播时，会发生相位变化。这种相位变化由传播常数的虚部表示，即

$\beta = \omega \sqrt{\left( \frac{\mu \epsilon}{2} \right) \sqrt{1 + \left( \frac{\sigma}{\omega \epsilon} \right)^2} + 1}$

此外，介质的本征阻抗可以表示为

$\eta = \sqrt{\frac{j\omega \mu}{\sigma + j\omega \epsilon}}$

自由空间中的均匀平面波

对于自由空间，$J = 0$，$\sigma = 0$，$\epsilon = \epsilon_0$，$\mu = \mu_0$，则传播常数的特性为：

$\alpha = 0$ $\beta = \omega \sqrt{\mu_0 \epsilon_0}$

因此，自由空间中的传播常数是纯虚数。

无损耗电介质中的均匀平面波

对于完美或无损耗电介质，其特性为 $\sigma = 0$，$\epsilon = \epsilon_0 \epsilon_r$，$\mu = \mu_0 \mu_r$。在自由空间介质和无损耗电介质中，$\sigma = 0$，因此这两种情况下的波的传播分析非常相似。但由于磁导率和介电常数的值不同，两种情况下的表达式也会有所不同。

传播速度为

$v = \frac{1}{\sqrt{\mu \epsilon}}$ $= \frac{1}{\sqrt{\mu_0 \mu_r \epsilon_0 \epsilon_r}} = \frac{1}{\sqrt{\mu_0 \epsilon_0} \sqrt{\mu_r \epsilon_r}} = \frac{1}{\sqrt{\mu_0 \epsilon_0} / \sqrt{\mu_r \epsilon_r}}$

因此，传播速度为

$v = \frac{c}{\sqrt{\mu_r \epsilon_r}} \, \text{m/s}$

传播常数为

$\gamma = \sqrt{j\omega \mu (\sigma + j\omega \epsilon)} \, \text{m}^{-1}$

将 $\sigma = 0$，$\epsilon = \epsilon_0 \epsilon_r$，$\mu = \mu_0 \mu_r$ 代入上述方程，对于完美或无损耗电介质，我们得到

$\gamma = \pm j\omega \sqrt{\mu \epsilon} \, \text{m}^{-1}$

同时，衰减常数 $\alpha = 0$。

相位常数为

$\beta = \omega \sqrt{\mu \epsilon} \, \text{rad/m}$

本征阻抗为

$\eta = \sqrt{\frac{j\omega \mu}{\sigma + j\omega \epsilon}} \, \text{ohms}$ $= \sqrt{\frac{\mu_0}{\epsilon_0}} \sqrt{\frac{\mu_r}{\epsilon_r}}$ $= \eta_0 \sqrt{\frac{\mu_r}{\epsilon_r}}$ $\eta = 377 \sqrt{\frac{\mu_r}{\epsilon_r}} \, \text{ohms}$

有损耗电介质中的均匀平面波

有损耗电介质是一种不良绝缘体，其中自由电荷会一定程度地传导。它是一种不完美的导体和不完美的电介质（部分导电介质），其电导率 $\sigma \neq 0$。

传播常数为

$\gamma = \sqrt{j\omega \mu (\sigma + j\omega \epsilon)}$

重新排列项，我们得到

$\gamma = \sqrt{j\omega \epsilon \left(1 + \frac{\sigma}{j\omega \epsilon}\right) j\omega \mu}$

因此，

$\gamma = \alpha + j\beta = j\omega \sqrt{\mu \epsilon} \sqrt{1 - j\left(\frac{\sigma}{\omega \epsilon}\right)}$

上述方程给出了有损耗电介质中的传播常数，由于根号因子的存在，它与无损耗电介质中的传播常数不同。通过代入 $\omega$、$\mu$、$\epsilon$ 和 $\sigma$ 的值，可以计算出衰减常数 $\alpha$ 和相位常数 $\beta$。

衰减常数 $\alpha$ 表示波在介质中的衰减程度，因此这种介质被称为有损耗电介质。

由于 $\sigma \neq 0$，本征阻抗成为一个复数，表示为

$\eta = \sqrt{\frac{j\omega \mu}{\sigma + j\omega \epsilon}}$ $\eta = |\eta| \angle \theta_n \, \text{Ohms}$

由于是复数，$\eta$ 以极坐标形式表示，如上式所示，其中 $\theta_n$ 是电场和磁场之间的相位角差。因此，在有损耗电介质中，电场和磁场之间存在相位差。

本征阻抗可以表示为

$\eta = \sqrt{\frac{j\omega\mu}{\sigma + j\omega\epsilon}}$ $= \sqrt{\frac{j\omega\mu}{j\omega\epsilon \left(1 + \frac{\sigma}{j\omega\epsilon}\right)}}$ $\eta = \left(\sqrt{\frac{\mu}{\epsilon}}\right) \left(\frac{1}{\sqrt{1 - j\left(\frac{\sigma}{\omega\epsilon}\right)}}\right) \, \Omega$

角度 $\Theta_n$ 为

$\Theta_n = \frac{1}{2} \left[\frac{\pi}{2} - \tan^{-1}\left(\frac{\omega\epsilon}{\sigma}\right)\right]$

这个角度取决于信号的频率以及损耗介质的特性。对于低频信号，$\omega$ 非常小，因此相位角为

$\Theta_n = \frac{\pi}{4}$

对于高频信号，$\omega$ 非常大，因此

$\Theta_n = 0$

所以，损耗介质在整个频率范围内的 $\Theta_n$ 范围是 $0 \leq \Theta_n \leq \frac{\pi}{4}$。

电磁波的应用

一般来说，波现象包含时变的电场和磁场。以下是一些可以遇到电磁波的应用领域。除了以下应用领域外，还有许多其他应用领域，在这些领域中，对电磁波的了解被广泛使用。

传输线

在低频电力传输的情况下，电阻、电容、电感等电气参数足以表征整个电路。在这种电路分析中，不考虑电气元件的物理尺寸，简单的基尔霍夫定律足以分析电路。

然而，如果频率增加，必须考虑物理参数的尺寸，空间也开始在电路分析中发挥作用。

在这种传输中，电压和电流以波的形式存在。这种包含空间考虑的电路分析方法被称为传输线方法。

天线

尽管天线看起来像是一个被动设备，但它却是通信系统中最重要的设备之一。它可以高效地发射和接收电磁波。多年来，为了满足不同的应用需求，已经使用了多种类型的天线。

随着移动通信技术的发展，近年来开发出了紧凑、多频段且高效的天线。这些天线通过使用从几瓦到兆瓦的功率来建立通信。

移动通信

了解无线环境需要掌握电磁波传播的知识。在蜂窝系统中，根据信号强度随距离变化的函数，采用不同的频率复用方案。移动通信的一个重要方面是衰落。

因此，为了准确预测衰落的行为，信号处理算法需要了解无线环境。因此，电磁波及其分析在移动通信系统中起着关键作用。

光纤通信

高速且高效的长途通信使用了多种光纤设备，这些设备利用了电磁波的复杂现象。这种通信是现代的导波通信形式。

为了研究光在光纤中的传播，使用了电磁理论。由于光的波性，光纤内出现了模态传播。此外，对于分析光电探测器和激光探测器，电磁波理论非常重要。

电磁干扰（EMI）与兼容性

一般来说，电路会产生电磁辐射，尤其是在切换大电流时。这种辐射可能会干扰网络中的其他部分或元件，从而影响整个电路的性能。

例如，开关电源（SMPS）和高速数字电路会产生相当大的电磁干扰。通常使用屏蔽电路来保护电路免受电磁干扰。因此，设计这种电磁干扰屏蔽需要了解电磁波。

射电天文学

射电天文学是物理学和电子工程学的结合。它是需要了解电磁波的一个主要领域。在天文学中，对天空的观测是在射频下进行的。

这些射频信号非常微弱，因此使用最先进的通信接收器和天线来检测这些信号。因此，在射电天文学中，电磁波的所有方面都被应用。