1.2 静磁学

与静电学（研究静止电荷，也称为库仑方法）相对，磁静学（magnetostatics）研究的是静止的电流（也称为安培方法）。1820年，科学家奥斯特（Oersted）发现了电场和磁场之间的关系。

他指出，当电荷处于运动状态时，其周围会产生磁场。因此，载流导体总是被磁场包围。如果导体中有恒定的或不随时间变化的电流通过，那么导体周围就会产生一个稳定的磁场。

这种恒定的电流实际上就是直流电（DC）。因此，研究由于恒定或直流电产生的稳定磁场的学科被称为磁静学。

什么是磁静学？

磁静学是研究在电流恒定或随时间保持稳定的情况下，磁场在系统中的行为。这一物理学领域考察由稳定（不变）电流所产生的磁场、磁力及其效应，为理解和设计各种依赖于静态条件下磁相互作用的电气设备和系统提供了基础。

磁场的基本原理

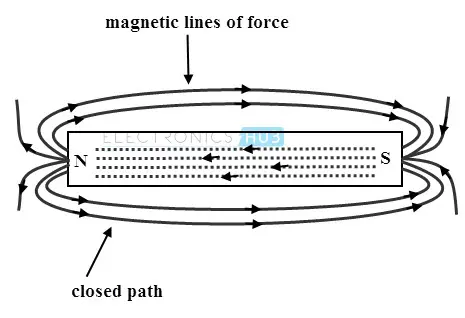
在学习磁场的基本概念之前，让我们先了解磁场的基本特性。考虑一个具有南北两极（分别记为N和S）的永磁体。磁体周围受其影响的区域被称为磁场。这个场实际上是围绕磁体的假想线的表示，这些线也被称为磁力线或磁通量线。著名的英国科学家迈克尔·法拉第（Michael Faraday）引入了这样的线，其方向是从磁体外部的北极指向南极。

磁通量线总是以闭合回路的形式存在，这意味着从北极出发的磁通量线必须终止于南极，无论磁场是由载流导体还是永磁体产生的。

由电流产生的磁场

我们知道，运动中的电荷构成电流，而运动中的电荷也会产生磁场。假设在一根直导体中有 $I$ 安培（直流电）的电流通过，那么沿着导体的整个长度，导体周围会产生一个磁场，该磁场的方向与电流垂直，呈圆形分布。

这些磁力线呈同心圆状，与导体垂直。磁力线的方向取决于导体中电流的方向。只要导体中有恒定且不随时间变化的电流通过，导体周围就会产生一个稳定的磁场。

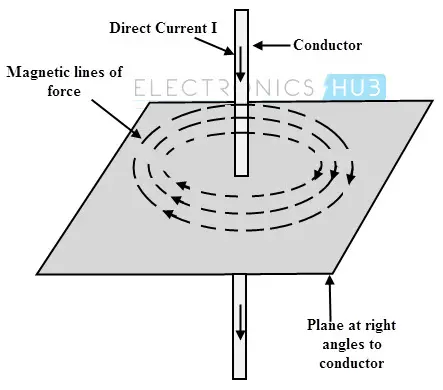
磁场的方向可以通过右手螺旋法则来确定。在这个方法中，磁场的方向由右手螺旋的方向给出，该螺旋需要沿着电流的方向前进。

另一个确定磁场方向的简便方法是右手定则。该定则指出，如果我们用右手握住导体，拇指指向电流方向且与导体平行，那么右手卷曲的其余手指给出的就是导体周围磁场的方向。

磁通密度

磁通密度用 $\overline{B}$ 表示，定义为单位面积上垂直于磁场方向的总磁力线或磁通量。它是一个矢量量，单位为每平方米的韦伯（Wb/m²），也称为特斯拉（T）。

磁场强度

磁场强度或磁场强度给出了磁场强弱的定量度量。它是一个单位北极（强度为1韦伯）在磁场中任意一点所受的力。它用 $\overline{H}$ 表示，单位为牛顿/韦伯（N/Wb）或安培·匝/米（AT/m）或安培/米（A/m）。

在磁静学中，磁场强度 $\overline{H}$ 和磁通密度 $\overline{B}$ 通过导体所在区域的磁导率相互关联。

该区域的磁导率允许载流导体在其周围产生磁通量。它用 $\mu$ 表示，单位为亨利/米（H/m）。这两个变量之间的关系为：

$\overline{B} = \mu \overline{H} = \mu_0 \mu_r \overline{H}$

其中 $\mu = \mu_0 \mu_r$。

对于自由空间，其磁导率用 $\mu_0$ 表示，其值为 $4\pi \times 10^{-7}$ H/m。$\mu_r$ 是相对磁导率，对于非磁性介质其值为1，对于磁性材料其值大于1。

洛伦兹力公式

稳定的磁场是由静止的电流产生的，而不是由静止的电荷产生的。因此，处于磁场中的运动电荷也会受到磁力的作用。洛伦兹力公式有助于确定带电粒子在电磁场中的受力情况。

该公式指出，如果一个电荷 $q$ 处于电场中，那么它所受的力等于电荷 $q$ 与电场强度 $E$ 的乘积。力的方向与磁场强度的方向一致。一个以速度 $v$ 运动的电荷 $q$ 所受的总力为：

$\mathbf{F} = q (\mathbf{E} + \mathbf{v} \times \mathbf{B}) \quad \text{牛顿}$

其中 $\mathbf{B}$ 称为磁通密度。这被称为洛伦兹力公式，它包含两部分，即电场力 $\mathbf{F}_e = q\mathbf{E}$ 和磁场力 $\mathbf{F}_m = q\mathbf{v} \times \mathbf{B}$。需要注意的是，电场力作用于静止和运动的电荷，而磁场力仅作用于运动的电荷。

此外，磁场不会向运动的带电粒子传递能量，而电场则会向带电粒子传递能量。

比奥-萨伐尔定律

比奥-萨伐尔定律给出了描述由电流产生的磁场的表达式。该定律由让-巴蒂斯特·比奥（Jean-Baptiste Biot）和菲利克斯·萨伐尔（Félix Savart）于1820年发现，并以他们的名字命名。

假设在导体中通入直流电，其周围会产生一个稳定的磁场。比奥-萨伐尔定律用于计算由于微分电流元 $I\,d\mathbf{l}$ 在点 $P$ 处产生的微分磁场强度 $d\overline{H}$。

假设微分长度为 $dL$，微分电流元为 $IdL$。微分电流元与点 $P$ 之间的距离为 $R$，$\theta$ 为微分电流元与连接点 $P$ 和微分电流元的直线之间的夹角。

根据比奥-萨伐尔定律，距离微分电流元 $IdL$ 为 $R$ 的点 $P$ 处产生的磁场强度与电流 $I$ 和微分长度 $dL$ 的乘积、夹角的正弦值成正比，与微分电流元和点 $P$ 之间距离 $R$ 的平方成反比。

数学表达式为：

$d\overline{H} \propto \frac{I\,dL\,\sin\theta}{R^2}$ $d\overline{H} = k \frac{I\,dL\,\sin\theta}{R^2}$

其中 $k$ 为比例常数，其值为 $\frac{1}{4\pi}$。

因此，

$d\overline{H} = \frac{I\,dL\,\sin\theta}{4\pi R^2} \quad \text{(1)}$

以矢量形式表示，设 $dL$ 为矢量长度 $\overline{dL}$ 的大小，

$\overline{a_R}$ 为从微分电流元指向 $P$ 点方向的单位矢量。

根据矢量叉乘规则，

$\overline{dL} \times \overline{a_R} = dL\,|\overline{a_R}|\,\sin\theta$ $= dL\,\sin\theta \quad \text{因为} \quad |\overline{a_R}| = 1$

代入上述公式得：

$d\overline{H} = \frac{I\,\overline{dL} \times \overline{a_R}}{4\pi R^2} \quad \text{A/m} \quad \text{(2)}$

但 $\overline{a_R} = \frac{\overline{R}}{R}$

因此，

$d\overline{H} = \frac{I\,\overline{dL} \times \overline{R}}{4\pi R^3} \quad \text{A/m} \quad \text{(3)}$

为了得到整个磁场强度，需要对公式 (2) 进行积分：

$\overline{H} = \oint \frac{I \, \overline{dL} \times \overline{a_R}}{4\pi R^2} \, \text{A/m}$

通过考虑电路的闭合路径（如图所示），两点之间的场强可以表示为

安培环路定律

安培环路定律与静电学中的高斯定律类似。利用该定律，可以在磁静学中解决复杂问题。该定律可用于计算由任意电流分布产生的磁场强度。

根据安培环路定律，磁场强度 $\overline{H}$ 在闭合路径上的线积分等于该路径所包围的电流。

数学表达式为：

$\oint \overline{H} \cdot \overline{dL} = I$

上述关系被称为安培环路定律的积分形式。

其中 $I$ 是闭合路径所包围的电流。

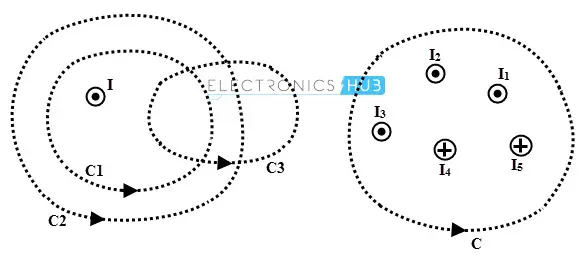
电流包围的概念在下图中展示，电流 $I$ 被闭合路径 $C_1$ 和 $C_2$ 所包围。因此，沿着这两个路径，场强的线积分结果均为 $I$。

然而，闭合路径 $C_3$ 并未包围任何电流，因此该回路的场强线积分为零。

在图 (b) 中，闭合路径 $C$ 被多条电流所包围，因此该闭合路径上的磁场强度 $\overline{H}$ 的线积分等于所有电流的代数和。

现在考虑电流在开表面上连续分布的情况，那么电流分布或电流密度 $J$ 为单位面积上的电流。因此，安培环路定律可以写为

因此，必须对所选闭合路径所包围的载流表面的面积进行面积积分。在下图中，路径 $C$ 上的场强线积分等于全部电流，而在第二幅图中，只有阴影区域给出了包围的电流。

因此，在将该定律应用于特定问题之前，有必要了解场的变化特性，以便选择合适的闭合路径。

磁静学能量

与电容器（在电场中储存能量）类似，电感器在磁场中储存能量。电感器储存的能量为

$W_m = \frac{1}{2} L I^2$

考虑上述图中，磁场 $B$ 存在于一个微分体积中。那么微分体积中的电感为

$\Delta L = \frac{\Delta \Phi}{\Delta I} = \frac{B \Delta S}{\Delta I}$

其中 $\Delta S$ = 微分表面积 = $\Delta x \Delta z$

$\Delta L = \frac{B (\Delta x \Delta z)}{\Delta I}$

微分电流 $\Delta I$ 可以用磁场强度 $H$ 表示为

$\Delta I = H \Delta y$（因为电流通过导电板的方向为 $y$ 方向）

因此，微分体积中的电感储存的能量为

$\Delta w_m = \frac{1}{2} \Delta L \Delta I^2$

代入 $\Delta L$ 和 $\Delta I$ 得

$\Delta w_m = \frac{1}{2} \left( \frac{B (\mu H \Delta x \Delta z)}{H \Delta y} \right) (H \Delta y)^2$ $\Delta w_m = \frac{1}{2} \mu H^2 (\Delta x \Delta y \Delta z)$

但微分体积 $\Delta v = (\Delta x \Delta y \Delta z)$

$\Delta w_m = \frac{1}{2} \mu H^2 \Delta v$

磁静学能量密度为

$w_m = \lim_{\Delta v \to 0} \left( \frac{\Delta w_m}{\Delta v} \right)$

因此

$w_m = \frac{1}{2} \mu H^2$

上述公式可以写成不同的形式：

$w_m = \frac{1}{2} (\mu H) H = \frac{1}{2} B H^2$ $w_m = \frac{1}{2} B \left( \frac{B}{\mu} \right) = \frac{1}{2} \frac{B^2}{\mu}$

线性介质中的磁静学场的能量为

$W_m = \int w_m \, dv$ $W_m = \frac{1}{2} \int \mu H^2 \, dv$ $W_m = \frac{1}{2} \int \frac{B^2}{\mu} \, dv$ $W_m = \frac{1}{2} \int B H \, dv$

磁路

磁路可以是串联的、并联的，或者是串联和并联的组合。一些实际的、常见的磁路包括变压器、电机、环形磁芯、发电机、继电器和磁记录设备。

串联磁路

考虑一个简单的磁路（如下图所示），它由均匀的横截面积 $A$、串联的磁通路径 $l$ 和长度为 $l_g$ 的小气隙组成。类似于电阻，磁通的阻碍称为磁阻，用 $R$ 表示。

下图也展示了等效电路。由于这是一个串联电路，相同的磁通量通过两种介质，即铁和空气。因此，对磁场提供的总磁阻将是空气和铁的磁阻之和。

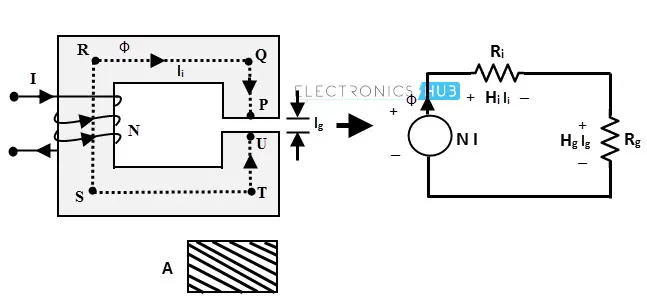
由于横截面积相同，磁通密度为 $\Phi / A$，在铁和空气路径中保持不变。但由于介质的磁导率不同，磁场强度 $H$ 也会不同。

铁所需的磁场强度，$H_i = \frac{B}{\mu_0 \mu_i}$

空气所需的磁场强度，$H_g = \frac{B}{\mu_0}$

根据安培环路定律，$N \cdot I = H_i l_i + H_g l_g$

$= \left( \frac{B}{\mu_0 \mu_i} \right) l_i + \left( \frac{B}{\mu_0} \right) l_g$ $= \left( \frac{\Phi}{\mu_0 \mu_i A} \right) l_i + \left( \frac{\Phi}{\mu_0 A} \right) l_g$ $N \cdot I = \Phi R_i + \Phi R_g$ $\Phi = \frac{N \cdot I}{R_i + R_g}$

从上述方程可以看出，磁阻是串联连接的。因此，在串联磁路中，总磁阻是个别磁阻的总和。

关于串联磁路需要注意的要点是，电路各部分的磁通量相同，等效磁阻是个别部分的磁阻之和，总磁动势（mmf）是每个部分的磁动势之和。

串联-并联磁路

如果一个磁路有多条磁通路径，则称为并联磁路。在这种磁路中，不同的磁阻可以是并联的。同样，也可以构建串联和并联电路的组合。考虑下图，它是一个串联和并联磁路的组合。

用于描述铁芯的垂直连接部分的术语是磁路的“肢”，用于描述铁芯的水平连接部分的术语是磁路的“轭”。从下图可以看出，PU、QT 和 RS 是肢，PQ、QR、UT 和 TS 是轭。在这里，总磁通被分为两个分量 $\Phi_1$ 和 $\Phi_2$。

磁通 $\Phi_1$ 通过路径 QTUP 完成闭合，磁通 $\Phi_2$ 通过路径 QRST 完成闭合。$\Phi_1$ 和 $\Phi_2$ 的相对值由各自路径的磁阻决定。

如果路径 TUPQ 的材料和横截面积相同，那么该路径的磁阻与 $l_{TUPQ} / A$ 成正比。

中心肢的磁通 $\Phi_1$ 遇到两种材料，即铁（QM 和 WT）和小气隙（MW）。

气隙的磁阻，$R_g = \frac{l_g}{\mu_0 A}$

磁性材料中心肢的磁阻为 $R_1 = R_{QM} + R_{WT}$。

携带磁通 $\Phi_2$ 的磁路部分的磁阻 $R_2$ 与 $l_{QRST} / A$ 成正比。

这里，$R_2 = R_{QRST}$。

下图展示了两个并联磁路路径的磁阻。

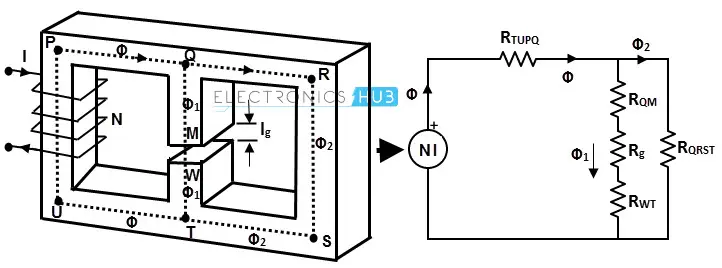
从上述电路中，可以得到以下结论：

总磁通量是各个磁通量的总和：

$\Phi = \Phi_1 + \Phi_2$

在回路 1 中的磁动势平衡为：

$NI = H_1 + H_1 l_1 + H_g l_g$ $= R \Phi + (R_1 + R_g) \Phi_1$

在回路 2 中的磁动势平衡为：

$(R_1 + R_g) \Phi_1 = R_2 \Phi_2$ $H_1 l_1 + H_g l_g = H_2 l_2$

在外部回路中的磁动势平衡为：

$NI = H_1 + H_2 l_2$