1.4 欧姆定律和功率

在分析直流电路时，我们通常使用不同的方法，如欧姆定律、网络定理和其他电路简化工具。直流电路分析的主要目的是确定与电子电路的一个或多个元件相关的未知量，如电压、电流、电阻和功率。作为简化电路的基本定律，欧姆定律定义了电压、电流和电阻之间的线性关系。让我们详细了解欧姆定律。

欧姆定律

欧姆定律是电学中的一个基本原理，描述了电路中电压、电流和电阻之间的关系。它指出，流过导体的电流与导体两端的电压成正比，与导体的电阻成反比。

欧姆定律通常用公式表示为：

$I = \frac{V}{R}$

在代数形式中：

$V \propto I$ $V = IR$

其中：

• $I$ 是流过电路的电流，以安培（A）为单位测量。
• $V$ 是施加在电路两端的电压，以伏特（V）为单位测量。
• $R$ 是比例常数，称为电阻，以欧姆（$\Omega$）为单位测量。

电阻也可以用千欧姆（k$\Omega$）、兆欧姆（M$\Omega$）等单位表示。

因此，欧姆定律表明，电路中的电流与电压成正比，与电阻成反比。欧姆定律可以应用于电路的各个部分或整个电路。

数学上：

$\text{电流}, I = \frac{V}{R}$ $\text{电压}, V = IR$ $\text{电阻}, R = \frac{V}{I}$

欧姆定律三角形

下图展示的欧姆定律三角形用于表示欧姆定律中不同量之间的关系。这是一种简单且易于记忆的方法，用于描述电压、电流和电阻之间的关系。

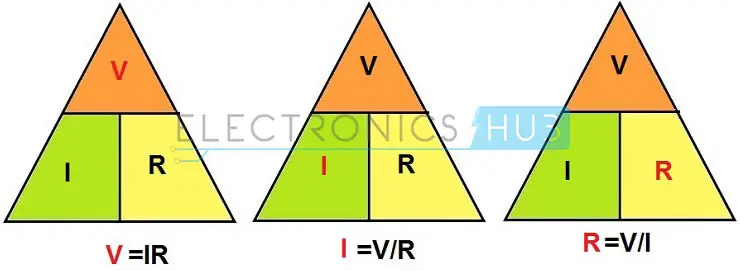
上图显示了欧姆定律三角形，其中电压、电流和电阻及其公式从基本的欧姆定律方程中表示。在上图中，一个参数可以根据另外两个参数计算得出。因此，可以得出结论：当电阻较高时，电流较小；当电阻较低时，电流较大，前提是施加的电压相同。

电功率

电功率表示电路传递能量的速率。电功率以瓦特（W）为单位测量。当电压导致电流在电路中流动时，电功率被消耗。

因此，电功率是电压和电流的乘积。

数学上：

$P = VI$

根据欧姆定律，$V = IR$ 和 $I = \frac{V}{R}$。

将这些代入功率方程中：

$P = I^2 R$ $P = \frac{V^2}{R}$

因此，电功率 $P$ 可以表示为 $VI$、$I^2 R$ 或 $\frac{V^2}{R}$。

这些是计算电路中电功率的三个基本公式。因此，当已知其中任意两个量时，可以计算出功率。

功率三角形

与欧姆定律三角形类似，下图展示了功率三角形，用于表示功率、电压和电流之间的关系。通过这个图，可以轻松记住各个参数的公式。隐藏或圆角的参数可以通过剩余两个参数的位置来确定，如下图所示。

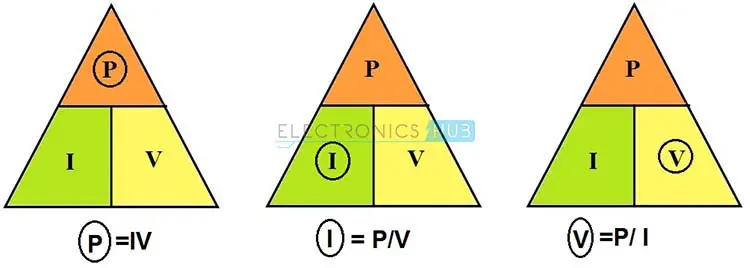
欧姆定律饼图

除了上述两个概念外，还有另一种方法可以使用欧姆定律来查找电路参数，即欧姆定律饼图。通过使用欧姆定律饼图，可以轻松记住用于查找电压、电流、电阻和功率的所有公式，这些公式对于简化电路（无论是简单电路还是复杂电路）都是必要的。

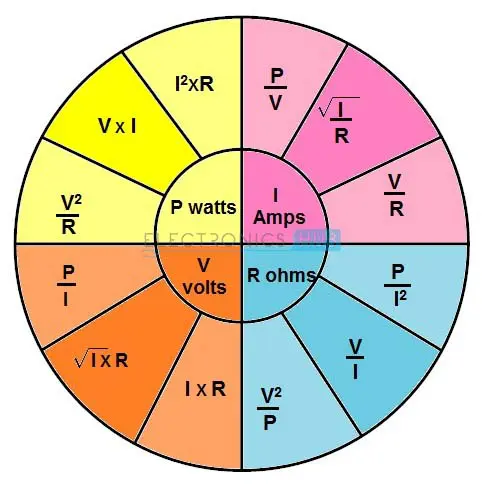
上图显示了饼图，它给出了功率、电压、电流和电阻之间的关系。这个图表分为四个部分，分别对应功率、电压、电阻和电流。每个部分包含三个公式，每个公式需要两个已知量。从图表中可以看出，对于电路中的每个参数，可以使用三个公式中的任意一个。

欧姆定律的图形表示

为了更好地理解这个概念，下面给出了一个实验装置，其中可调电压源（每个单元2V，共六个单元）通过电压选择开关连接到负载电阻。测量仪器（如伏特表和安培表）也连接到电路中，用于测量电路中的电压和电流。

首先连接10欧姆的电阻，并将选择开关置于位置1。此时，安培表读数为0.2A，伏特表读数为2V，因为 $I = \frac{V}{R}$，即 $I = \frac{2}{10} = 0.2A$。接下来，将选择开关切换到第二个单元，将4V施加到负载上，并记录安培表的读数。随着选择开关从第一个位置逐步切换到最后一个位置，我们将得到对应的电流值：2V、4V、6V、8V、10V 和 12V 时的电流分别为 0.2A、0.4A、0.6A、0.8A、1A 和 1.2A。

接下来，用20欧姆的电阻替换10欧姆的电阻，并重复上述过程。我们将得到对应的电流值：2V、4V、6V、8V、10V 和 12V 时的电流分别为 0.1A、0.2A、0.3A、0.4A、0.5A 和 0.6A。将这些值绘制成图，如下所示。

在上图中，对于给定的电压，当电阻较大时，电流较小。考虑施加12V电压的情况，当电阻为10欧姆时，电流值为1.2A；而当电阻为20欧姆时，电流值为0.6A。同样，对于相同的电流流动，当电阻较大时，电压也较大。从上述结果可以看出，当电阻恒定时，电压与电流的比值是恒定的。因此，电压与电流之间的关系是线性的，且随着电阻的增大，这条直线的斜率变得更陡。

欧姆定律示例

考虑下图所示的电路，其中6V的电池连接到6欧姆的负载。安培表和伏特表连接到电路中，用于实际测量电流和电压。但使用欧姆定律，我们可以如下计算电流和功率。

根据欧姆定律：

$V = IR$ $I = \frac{V}{R}$ $I = \frac{6}{6}$ $I = 1 \text{安培}$

功率 $P = VI$

$P = 6 \times 1$ $P = 6 \text{瓦特}$

但实际上，由于电池的内阻，安培表不会显示精确值。考虑电池的内阻（假设电池内阻为1欧姆），电流值可以如下计算。

电路的总电阻为 6 + 1 = 7 欧姆。

电流 $I = \frac{V}{R}$

$I = \frac{6}{7}$ $I = 0.85 \text{安培}$

汽车前大灯电路

下图展示了汽车前大灯电路（不包括控制电路）。通过应用欧姆定律，我们可以计算出每个灯泡的电流。通常，每个灯泡都与电池并联连接，即使其中一个灯泡损坏，其他灯泡仍然可以发光。一个12V的电池为这些并联灯泡供电，每个灯泡的电阻为2.4欧姆（在此假设）。

电路的总电阻为 $R = \frac{R1 \times R2}{R1 + R2}$，因为它们是并联的。

$R = \frac{5.76}{4.8} = 1.2$

流过电路的电流为 $I = \frac{V}{R}$

$I = \frac{12}{1.2}$ $I = 10A$

流过每个灯泡的电流为 $I1 = I2 = 5A$（由于电阻相同）。

欧姆定律在交流电路中的应用

一般来说，欧姆定律也可以应用于交流电路。如果负载是电感性或电容性的，则需要考虑负载的电抗。因此，通过考虑电抗的影响并对欧姆定律进行一些修改，可以将其应用于交流电路。在交流电路中，由于电感和电容的存在，电压和电流之间会有相当大的相位角。此外，交流电路中的电阻称为阻抗，用 $Z$ 表示。

因此，交流电路中的欧姆定律为：

$E = IZ$ $I = \frac{E}{Z}$ $Z = \frac{E}{I}$

其中 $E$ 是交流电路中的电压，$I$ 是电流，$Z$ 是阻抗。

上述方程中的所有参数均以复数形式表示，包括相位角。类似于直流电路的欧姆定律饼图，交流电路的欧姆定律饼图如下所示。

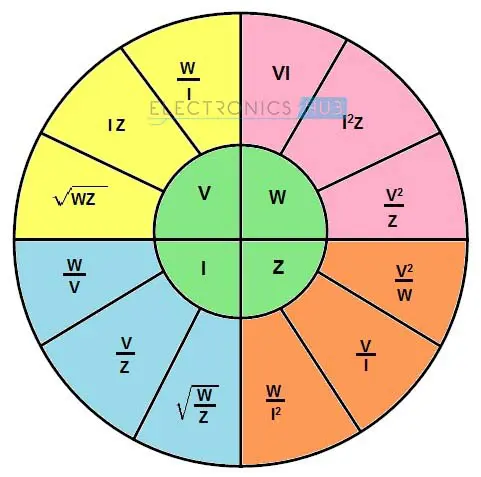
欧姆定律示例（交流电路）

考虑下图所示的电路，其中交流负载（电阻性和电感性组合）连接到10V、60Hz的交流电源。负载的电阻值为5欧姆，电感为10毫亨。

负载的阻抗值 $Z$ 为：

$Z = R + jX_L$ $Z = 5 + j(2\pi f L)$ $Z = 5 + j(2 \times 3.14 \times 60 \times 10 \times 10^{-3})$ $Z = 5 + j3.76 \, \Omega$

或以6.26欧姆的阻抗在-37.016°的相位角表示。

流过电路的电流为：

$I = \frac{V}{Z}$ $I = \frac{10}{5 + j3.76}$

$I = 1.597 \, \text{A}$ 在-37.016°的相位角。