1.3 直流电路基础知识

能够处理交流（AC）或直流（DC）的电路是由有源元件（电源）和无源元件（电阻、电容和电感）组成的。因此，电路理论或分析有助于通过使用不同技术找出电路中各种元件的电压和电流，从而理解电路的行为或特性。在我们深入探讨直流电路理论之前，让我们先简要讨论一下电学的基本概念。

电学的基本概念

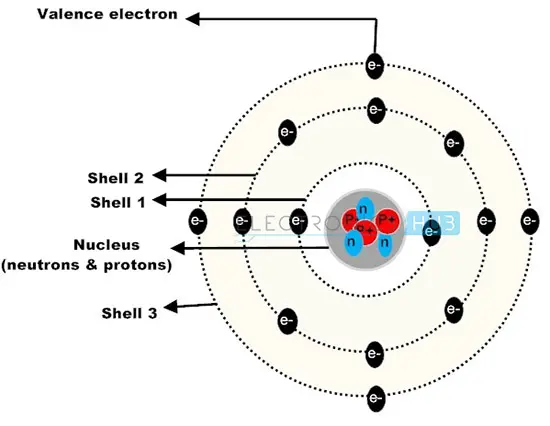
根据原子理论，所有物质都是由原子构成的。根据尼尔斯·玻尔原子模型，原子由一个带正电的中心核和围绕其旋转的电子组成。原子核由中子和带正电的质子组成。电子是带负电的粒子，围绕原子核旋转。原子中的质子和电子数量相等，这些相反电荷之间存在强大的吸引力，使得电子围绕原子核旋转。

玻尔模型给出了原子各层中电子的分布。最重要的是价电子层，即最外层的电子层，最多包含八个电子。这些电子距离原子核最远，因此需要额外的能量才能使它们脱离原子。这些电子的流动产生了电流。然而，最外层价电子层中的电子数量决定了电流的流动，因为该层的能量由其中的电子共享。如果价电子层有八个电子，每个电子将拥有该层能量的八分之一。

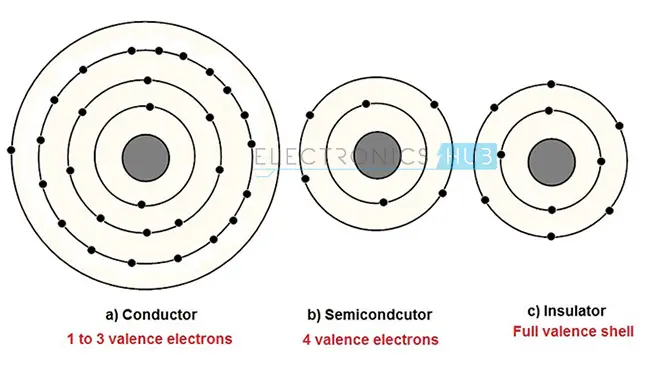
因此，需要大量的外部能量才能使电子脱离原子，从而产生电流。通常，最外层没有自由电子的材料被称为绝缘体。典型的绝缘体在其价电子层中有五到七个价电子。另一方面，具有一个价电子的材料只需要少量能量就能使电子脱离，从而产生电流，这些材料被称为导体。典型的导体在其价电子层中有两个或三个价电子。这些良好的导体包括银、铜、铝、金等。此外，具有四个价电子的材料既具有导体又具有绝缘体的特性，被称为半导体。

根据上述原子理论，电子的流动产生了电流。我们知道，同性电荷相互排斥，异性电荷相互吸引。在电源的作用下，电荷的分离使得负电荷在一端积累，正电荷在另一端积累。当在两个电荷之间建立通路时，电流开始流动。电荷的单位是库仑，它包含 $6.25 \times 10^{18}$ 个电子。外加的力或电压导致电荷移动，电荷流动的速度由施加的电压量决定。

直流电路基础和参数

我们知道，电流有两种类型：交流（AC）和直流（DC）。处理交流电的电路被称为交流电路，而带有直流电源的电路被称为直流电路。目前，我们只讨论直流电路及其理论。直流电源允许电流以不变的极性流动，这种极性不会随时间变化。下面的简单直流电路可以帮助读者了解直流电路的元件及其参数。

上述直流电路包括电压源和电阻，以及特定的电流流动。让我们简要了解一下这些参数。

1. 电动势（电压） 电路中两点之间的电势差或电压是将单位电荷从一点移动到另一点所需的能量。它以伏特为单位测量，并用字母 $V$ 表示，如下图所示。这种电压可以是正的也可以是负的，通常用前缀如 kV、mV、μV 等表示电压的子倍数。电池和发电机是最常用的直流电压源，它们可以产生从 1V 到 24V 的直流电压，以供一般电子电路运行。

2. 电流 电流是电子或电荷的流动。它以安培（A）为单位测量，并用字母 $I$ 或小写 $i$ 表示。这种电流可以是直流（DC）或交流（AC）。直流（DC）电流单向流动，通常由电池、太阳能电池、热电偶等产生。在交流（AC）中，电荷的运动周期性变化，如正弦波所示。

通常在电路中，电流流动的方向用字母 $I$ 或小写 $i$ 表示，并附有箭头。但这个方向实际上表示的是传统电流流动方向，而不是实际的电子流动方向。

3. 传统电流与电子流动方向的区别 电子从负极流向正极被称为电子流动方向，而从正极流向负极被称为传统电流流动方向，如下图所示。

电子总是被负电荷排斥，因此当负极连接到电池的负极时，电子被正极的正电荷吸引。因此，电子从负极流向正极被称为电子流动方向。然而，传统上假设电流从正极流向负极，因此这被称为传统电流流动方向。许多电路图上标示的是传统电流方向，而在描述单个电流流动时则标示实际的电子流动方向。

传统电流流动是由于正电荷载流子引起的。传统电流与实际电子流动方向相反，因为实际电子流动是由负电荷载流子（电子）引起的，因此传统电流总是正的。它也以安培为单位测量。

传统电流与实际电子流动方向的差异不会影响任何计算结果和实际行为。大多数直流电路分析结果与电流流动方向无关。然而，传统电流是标准且最常遵循的。

4. 电阻 导电材料的电阻阻碍了电子的流动。它以欧姆为单位测量，并用希腊字母 $\Omega$ 表示。根据电路中的电阻值，决定施加到电路的电压。因此，电阻可以定义为使电路中产生 1 安培电流所需的电压。这也可以称为欧姆定律，公式为 $R = \frac{V}{I}$。这意味着如果一个电路需要 200V 来产生 2A 的电流，那么电阻应该是 100 欧姆。电阻值总是正的。电阻可以是固定的，也可以是可变的，如下图所示。

5. 电功率（P）和能量 功率是指在给定时间内完成的工作量。在电路中，功率等于电压和电流的乘积。因为电压是单位电荷所做的功，电流是电路中电子流动的速度。功率以瓦特（W）为单位测量，其公式为

   $P = I \times V$

   根据欧姆定律，

   $R = \frac{V}{I}$ $V = I \times R$

   将上述公式代入，

   $P = (I \times R) \times I$ $P = I^2 \times R$

   或者，通过代入 $I = \frac{V}{R}$，我们也可以得到

   $P = V \times \left(\frac{V}{R}\right)$ $P = \frac{V^2}{R}$

   这三个公式用于计算与电路相关的功率。

   电能 电能消耗的速率通常被称为电能。电能以瓦特秒为单位测量，因为功率以瓦特为单位，时间以秒为单位。通常它以千瓦时为单位测量，正如我们在家庭电表中看到的那样。

   电能 = 功率 × 时间

   电学参数计算示例

   考虑一个额定功率为 100W 的电灯泡连接到 250V 的电源。计算流向负载的电流、灯泡的电阻以及在两分钟内散发的能量。

从功率公式我们知道 $P = V \times I$

那么流经灯泡的电流为：

$I = \frac{100}{250}$ $I = 0.4 \, \text{A}$

根据欧姆定律，

$R = \frac{V}{I}$ $R = \frac{250}{0.4}$ $R = 625 \, \Omega$

消散的能量为：

$E = \text{功率} \times \text{时间}$ $E = V \times I \times t$ $E = 250 \times 0.4 \times (2 \times 60)$ $E = 12000 \, \text{瓦特秒}$