跳到主要内容

1.7 维恩桥振荡器

由于具有良好的频率稳定性、极低的失真以及易于调谐等优点，惠斯通电桥振荡器成为了最受欢迎的音频频率范围信号发生器电路。这种振荡器使用了RC反馈网络，因此也可以被视为一种RC振荡器。

一般振荡器与惠斯通电桥振荡器的主要区别在于，在一般振荡器中，放大器阶段引入了180度的相移，而反馈网络又额外引入了180度的相移，从而在环路中实现了360度或零度的相移，以满足巴克豪森准则。

然而，在惠斯通电桥振荡器的情况下，放大器阶段使用的非反相放大器不引入任何相移。因此，为了满足巴克豪森准则，反馈网络不需要引入相移。让我们简要讨论一下惠斯通电桥振荡器。

惠斯通电桥振荡器​

惠斯通电桥振荡器产生正弦波，使用RC网络作为电路的频率决定部分。带有放大器阶段的基本惠斯通电桥振荡器电路如下图所示。

放大器的输出被施加在1和3端之间，而放大器阶段的输入则从2和4端供给。因此，放大器的输出成为电桥的输入电压，而电桥的输出则成为放大器的输入电压。

alt text

当电桥平衡时，放大器的输入电压变为零。因此，为了产生持续的振荡，放大器的输入必须是非零的。通过调整电阻的适当值，使电桥不平衡。

正如我们上面提到的，RC网络负责决定振荡器的频率。这个RC网络由两个频率敏感的臂组成，即串联的 R1C1R_1C_1 和并联的 R2,C2R_2, C_2。这个网络也被称为超前 - 滞后电路。

alt text

在滞后电路中，电容两端的输出电压滞后于输入电压一个介于0到 - 90度之间的角度。在超前电路中，电阻两端的输出电压超前于输入电压一个介于0到90度之间的角度。

在极低频率下，由于串联电容表现为开路，输出电压变为零；而在极高频率下，由于并联电容表现为短路，输入电压的路径被短路，因此也没有输出。因此，在这两种极端条件之间，输出电压达到最大值。

谐振频率是输出电压最大的频率。在这个频率下，反馈分数 KK 达到最大值1/3。

当 Xc=RX_c = R 时，反馈最大，因此谐振频率由下式给出：

f=12πRCf = \frac{1}{2\pi RC}
alt text

上图显示了谐振频率下的输出电压。在谐振频率下，电路的相移为零，衰减 V1/V0V_1/V_0 为1/3。因此，为了维持振荡，放大器必须具有大于3的增益。

通过将两个电容器安装在轴上，并同时改变它们的值，惠斯通电桥振荡器可以提供不同的频率范围。

使用运算放大器的惠斯通电桥振荡器​

下图展示了一种广泛使用的惠斯通电桥振荡器。运算放大器被配置为非反相放大器，反馈来自一个电压分配网络。电阻 R1R_1 和 RfR_f 构成了反馈路径的一部分，用于确定或调整放大器的增益。

运算放大器的输出连接到电桥的输入端 aa 和 cc，而电桥的输出端 bb 和 dd 则连接到运算放大器的输入端。

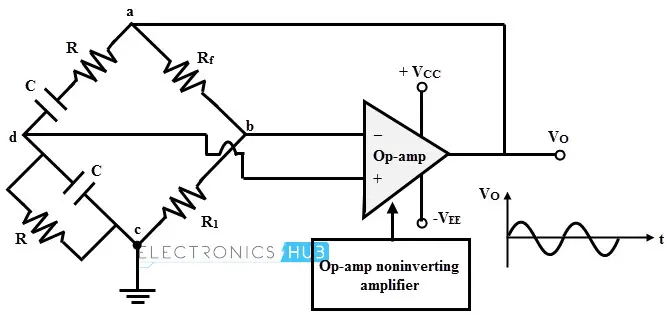
alt text

放大器输出的一部分通过电压分配网络（电阻和电容的串联组合）反馈到放大器的正或非反相端。

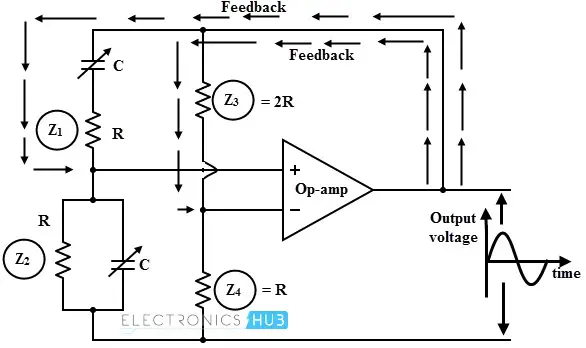
此外，放大器的第二部分通过阻抗大小为 2R2R 的路径反馈到放大器的反相或负端。

如果正确选择了反馈网络元件，则在某个频率下，输入到放大器的信号的相移为零。由于放大器是非反相的，引入了零相移，加上反馈网络的零相移，环路中的总相移变为零，从而满足了振荡所需的条件。

因此，惠斯通电桥振荡器作为一个正弦波发生器，其振荡频率由 RR 和 CC 元件决定。

alt text

运算放大器的增益表示为：

A=1+RfR1A = 1 + \frac{R_f}{R_1}

正如我们上面讨论的，非反相放大器的增益必须至少为3，以满足巴克豪森准则。

因此，

1+RfR1≥31 + \frac{R_f}{R_1} \geq 3
RfR1≥2\frac{R_f}{R_1} \geq 2

因此，电阻 RfR_f 与 R1R_1 的比值必须等于或大于2。振荡频率由下式给出：

f=12πRCf = \frac{1}{2\pi RC}

惠斯通电桥振荡器示例问题​

确定惠斯通电桥振荡器电路的 RR 和 CC 值，使其在10 kHz的频率下工作，已知 R=100 kΩR = 100 \ \text{k}\Omega，R1=1 kΩR_1 = 1 \ \text{k}\Omega。

已知 f=10 kHzf = 10 \ \text{kHz}，R=100 kΩR = 100 \ \text{k}\Omega，R1=1 kΩR_1 = 1 \ \text{k}\Omega。

惠斯通电桥振荡器的振荡频率由下式给出：

f=12πRCf = \frac{1}{2\pi RC}

因此，

C=12π×100×103×10×103=0.159 nFC = \frac{1}{2\pi \times 100 \times 10^3 \times 10 \times 10^3} = 0.159 \ \text{nF}

为了维持振荡，增益必须大于3，即 A≥3A \geq 3。

因此，

1+RfR1≥31 + \frac{R_f}{R_1} \geq 3
RfR1≥2\frac{R_f}{R_1} \geq 2
Rf≥1 kΩR_f \geq 1 \ \text{k}\Omega

因此，RR 和 CC 的值分别为 0.159 nF0.159 \ \text{nF} 和 1 kΩ1 \ \text{k}\Omega。

晶体管化惠斯通电桥振荡器​

下图展示了一个使用两级共发射极晶体管放大器的晶体管化惠斯通电桥振荡器。每个放大器阶段引入180度的相移，因此总共引入了360度的相移，这实际上就是零相移条件。

反馈电桥由RC串联元件、RC并联元件以及 R3R_3 和 R4R_4 电阻组成。电桥电路的输入从晶体管 T2T_2 的集电极通过耦合电容施加。

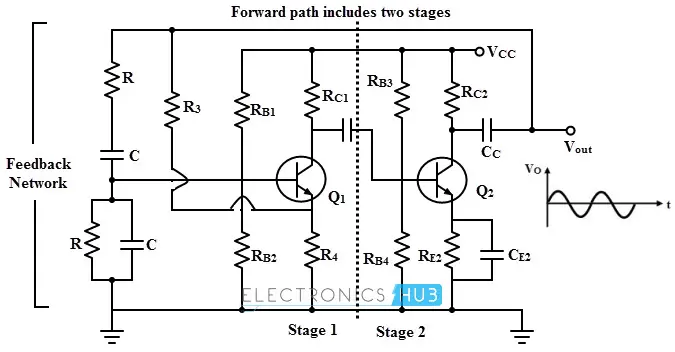
alt text

当直流电源施加到电路时，由于电荷载流子通过晶体管和其他电路元件的运动，在晶体管 T1T_1 的基极产生了一个噪声信号。这个电压被放大，增益为 AA，并产生与输入电压相位差180度的输出电压。

这个输出电压被作为输入施加到第二个晶体管 T2T_2 的基极。这个电压被 T2T_2 的增益放大。

晶体管 T2T_2 的放大输出与 T1T_1 的输出相位差180度。这个输出通过耦合电容 CC 反馈到晶体管 T1T_1。因此，当满足巴克豪森条件时，通过这种正反馈在宽频率范围内产生振荡。

一般来说，反馈网络中的惠斯通电桥在单一期望频率下产生振荡。

电桥在总相移为零的频率下达到平衡。

两个阶段的晶体管输出作为反馈网络的输入，该输入施加在基极和地之间。

反馈电压，Vf=Vo×R4R3+R4V_f = \frac{V_o \times R_4}{R_3 + R_4}

惠斯通电桥中的自动增益控制​

为了实现反馈振荡器的稳定性，增益必须能够自我调节。这是一种自动增益控制（AGC）。可以通过简单地在反馈网络中与电阻 R3R_3 并联一个齐纳二极管来实现。当输出信号达到齐纳击穿电压时，齐纳二极管导通，从而短路电阻 R3R_3。

这将放大器增益降低到3，因此由于总环路增益为1，从而产生持续的振荡。尽管这种自动增益控制方法很简单，但它受到齐纳二极管非线性的影响，因此正弦波会失真。

另一种控制增益的方法是使用JFET（结型场效应晶体管）作为负反馈路径中的电压控制电阻。与齐纳二极管方法相比，这种增益控制方法可以产生稳定的正弦波形。JFET在小信号或零偏置电压（VosV_{os}）的欧姆区工作。

因此，随着栅极电压的增加，漏极 - 源极电阻也会增加。当JFET放置在负反馈环路中时，通过这种电压控制电阻实现了自动增益控制。

alt text

上图展示了JFET稳定的惠斯通电桥振荡器的自动增益控制。在这个电路中，放大器的增益由元件 RfR_f、R3R_3 和 Q1Q_1 控制。根据栅极电压的不同，漏极 - 源极电阻会发生变化。当栅极电压为零时，该电阻最小。此时，环路增益将大于1。

随着输出电压的迅速增加，负输出信号会使二极管正向偏置，从而使电容充电至负电压。这种充电电压会增加JFET漏极与源极之间的电阻，进而导致放大器增益降低。

通过选择合适的反馈元件值，可以将环路增益稳定在所需的水平。

优点​

  • 由于使用了两级放大器，该振荡器的整体增益较高。
  • 通过改变 C1C_1 和 C2C_2 的值或使用可变电阻，可以调节振荡频率。
  • 它能够产生失真较小的优质正弦波。
  • 频率稳定性良好。
  • 由于没有使用电感，因此不会受到外部磁场的干扰。

缺点​

  • 两级放大器类型的惠斯通电桥振荡器需要更多的元件。
  • 无法产生非常高的频率。