1.8 微分放大器
在本教程中,我们将学习运算放大器作为微分器(或微分放大器)的工作原理和实现方法。微分放大器可以是无源的或有源的,这取决于其设计中使用的元件。将运算放大器配置为微分器或微分放大器,本质上是将运放用作高通滤波器,它被广泛应用于波形整形电路、频率调制器等。
在另一个教程中,我们已经讨论了运算放大器作为积分器的应用,学习了如何将运算放大器配置为积分器。在这里,我们将进行类似的分析,但这次针对的是运算放大器作为微分器。
关于无源高通滤波器的更多信息,请阅读《无源高通 RC 滤波器》和《有源高通滤波器》。有关运放的基础知识,请参阅《运算放大器基础》。
运放微分器
运放微分器或微分放大器是一种与积分器电路相反的电路配置。它产生一个输出信号,其瞬时幅度与施加的输入电压的变化率成正比。
从数学上讲,微分器的输出信号是输入信号的一阶导数。例如,如果输入信号是一个锯齿波,那么以运放作为微分器的电路输出将是简单的直流电(因为锯齿波信号的变化率是恒定的)。同样,如果输入信号是一个正弦波,那么输出信号也是一个正弦波,但相位差为90°。
仅使用 RC 网络的微分器称为无源微分器,而使用有源电路元件(如晶体管和运算放大器)的微分器称为有源微分器。有源微分器比简单的 RC 微分器具有更高的输出电压和更低的输出电阻。
运放微分器是一种反相放大器,它在输入电压中串联了一个电容器。微分电路通常被设计为对三角波和矩形波输入波形做出响应。
在处理正弦波输入时,微分器存在频率限制;该电路衰减所有低频信号分量,仅允许高频分量出现在输出端。换句话说,该电路表现得像一个高通滤波器。
理想运放微分器电路
运放微分放大器在输入电压源中串联了一个电容器,如下图所示。
对于直流输入,输入电容器 在达到其电势后,无法接受任何电荷,表现得像开路。运放的非反相输入端通过电阻 接地,提供输入偏置补偿,反相输入端通过反馈电阻 连接到输出端。
因此,该电路表现得像一个电压跟随器。
当输入是一个正向电压时,电流 流入电容器 ,如下图所示。由于流入运放内部电路的电流为零,实际上所有电流 都流经电阻 。输出电压为
这里,输出电压与输入电压的变化率成正比。
从图中可以看出,节点“X”被虚拟接地,节点“Y”也处于地电位,即
从输入端来看,电流 可以表示为:
从输出端来看,电流 表示为:
将上述两个电流方程相等,我们得到:
上述方程表明,输出是输入电压的微分的 倍。乘积 称为微分器电路的 RC 时间常数。负号表示输出与输入相位相差180°。
这种有源微分放大器电路的主要优点是微分所需的较小时间常数。
输入和输出波形
现在我们来看不同输入信号的输出波形。当将幅度为 的阶跃输入(直流电平)施加到运放微分器时,输出可以表示为
为了简化,假设 的乘��积为1。
因此,,因为幅度 是恒定的,且 。
但实际上,输出并不为零,因为输入阶跃波从0伏特上升到 伏特需要有限的时间。因此,输出在 时出现一个尖峰,如下图所示。
如果将微分器的输入改为方波,则输出将是一个包含正负尖峰的波形,对应于电容器的充放电,如下图所示。
对于正弦波输入,其数学表达式为 ,其中 是输入信号的幅度, 是周期,微分器的输出为
为了简化,假设 的乘积为1。
因此,微分器对于正弦波输入的输出是一个余弦波,输入和输出波形如下图所示。
理想微分器的频率响应
运放微分器的增益直接取决于输入信号的频率。因此,对于直流输入(),输出也为零。随着输入信号频率的增加,输出也随之增加。理想微分器的频率响应如下图所示。
频率 是微分器增益变为1的频率。从图中可以看出,对于小于 的频率,增益小于1。对于 ,增益变为1(0 dB),并且超过 后,增益以每十倍频程20 dB的速率增加。
实际运放微分器电路
对于理想微分器,随着频率的增加,增益也会增加。因此,在某些较高频率下,微分器可能会变得不稳定并引起振荡,从而产生噪声。
在实际微分器电路中,可以通过使用与输入电容器串联的电阻 和与反馈电阻并联的电容器 来避免或纠正这些问题,如下图所示。
实际运放微分器电路的输出电压表示为
即,输出电压是输入电压微分的 倍。
添加电阻 和电容器 可以在较高频率下稳定电路,并减少噪声对电路的影响。
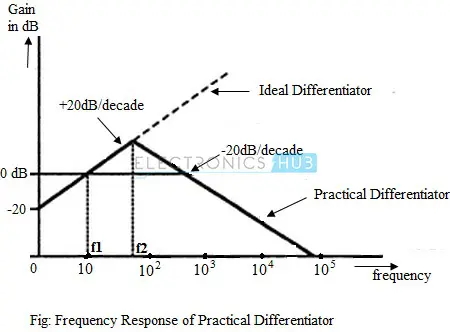
实际微分器的频率响应
实际微分器的增益随着频率的增加而增加,在特定频率 处,增益变为1(0 dB)。增益继续以每十倍频程20 dB的速率增加,直到输入频率达到频率 。
超过这个输入信号频率后,微分器的增益开始以每十倍频程20 dB的速率减小。这种效果是由于添加了电阻 和电容器 。实际微分器的频率响应曲线如下图所示。
运放微分器的应用
微分放大器通常被设计为对三角波和矩形波信号进行操作。
微分器还被应用于波形整形电路,以检测输入信号中的高频分量。
运放微分器总结
运放微分放大器是一种反相放大器电路配置,它使用反应元件(通常是电容器而非电感器)。
微分器对输入信号执行随时间的数学微分运算,即瞬时输出电压与输入信号的变化率成正比。
微��分电路通常用于对三角波和矩形波信号进行操作。在处理正弦波输入时,微分电路存在频率限制。