跳到主要内容

1.7 积分放大器

运放的另一个主要应用是其在数学运算中的使用。运算放大器可以配置为执行积分和微分等数学运算。事实上，“运算放大器”这一名称就来源于其用于执行数学运算的功能。在本教程中，我们将学习和分析运算放大器作为积分器的工作原理。

在之前的教程中，我们已经了解了运算放大器如何作为微分器工作。有关该主题的更多信息，请阅读《运算放大器作为微分器》。

运放的配置​

运算放大器可以配置为执行微积分运算，如微分和积分。在积分电路中，输出是输入电压随时间的积分。无源积分器是一种不使用运放或晶体管等有源器件，而仅使用电阻和电容等无源元件的电路。

包含有源器件的积分电路称为有源积分器。有源积分器可以提供比简单 RC 电路更低的输出电阻和更高的输出电压。

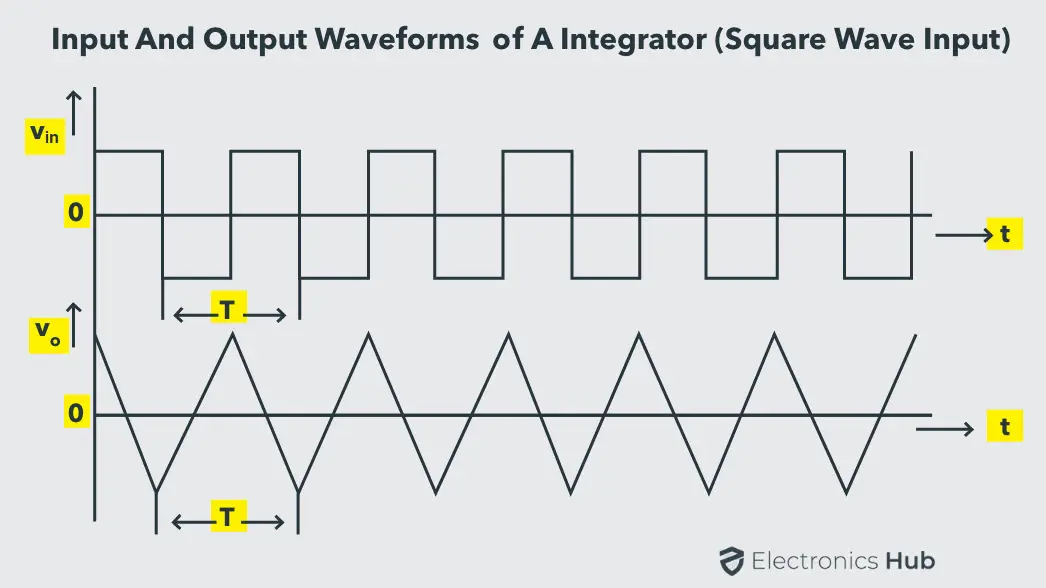
运放的微分和积分电路本质上是反相放大器，在适当位置放置了电容器。积分电路通常设计为从方波输入产生三角波输出。

积分电路在处理正弦波输入信号时存在频率限制。

理想运放积分器电路​

运算放大器积分器电路产生一个与波形下的面积（幅度乘以时间）成正比的输出电压。

理想运放积分器使用一个电容器 CfC_f，连接在输出端和运放的反相输入端之间，如下图所示。

alt text

反相输入端的负反馈确保节点 X 保持在地电位（虚拟地）。如果输入电压为 0 V，则输入电阻 R1R_1 中没有电流，电容器未充电。

因此，输出电压理想上为零。

如果在积分放大器的输入端施加一个恒定的正电压（直流电），输出电压将以线性速率下降，试图保持反相输入端在地电位。

相反，输入端的恒定负电压会导致输出电压线性上升（正向）。输出电压的变化率与施加的输入电压值成正比。

输出电压计算​

从电路中可以看出，节点 Y 通过补偿电阻 R1R_1 接地。由于虚拟地的存在，节点 X 也将处于地电位。

VX=VY=0V_X = V_Y = 0

由于运放的输入电流理想上为零，因此由于 VINV_{IN} 流经输入电阻的电流也流经电容器 CfC_f。

从输入端来看，电流 II 表示为：

I=VIN−VXR1=VINR1I = \frac{V_{IN} - V_X}{R_1} = \frac{V_{IN}}{R_1}

从输出端来看，电流 II 表示为：

I=Cfd(VX−VOUT)dt=−Cfd(VOUT)dtI = C_f \frac{d(V_X - V_{OUT})}{dt} = -C_f \frac{d(V_{OUT})}{dt}

将上述两个 II 的方程相等，我们得到：

VINR1=−Cfd(VOUT)dt\frac{V_{IN}}{R_1} = -C_f \frac{d(V_{OUT})}{dt}

对上述方程的两边进行积分：

alt text

在上述方程中，输出是输入电压的积分的 −1R1Cf-\frac{1}{R_1 C_f} 倍，其中 R1CfR_1 C_f 称为积分器的时间常数。

负号表明输入和输出之间存在 180° 的相位差，因为输入被施加到运放的反相输入端。

积分器放大器作为锯齿波发生器​

如果将积分放大器的阶跃输入替换为连续时间方波，输入信号幅度的变化将对反馈电容器进行充放电。

这将产生一个三角波输出，其频率取决于 R1CfR_1 C_f 的值，这被称为电路的时间常数。这种电路通常被称为锯齿波发生器。

在方波输入的正半周期间，恒定电流 II 流经输入电阻 R1R_1。由于流经运放内部电路的电流为零，实际上所有电流都流经反馈电容器 CfC_f。这个电流对电容器进行充电。

由于电容器连接到虚拟地，电容器两端的电压就是运放的输出电压。

在方波输入的负半周期间，电流 II 反转。电容器现在线性充电，产生一个正向锯齿波输出。

alt text

交流运放积分器​

如果向运算放大器积分器提供一个频率变化的正弦波输入，积分器表现得像一个“低通滤波器”，仅在输出端产生低频信号。所有高频信号分量都被阻断或衰减。

在 0 Hz 时，反馈电容器表现得像开路，因此没有从输出到运放反相输入端的反馈。此时，电路表现得像一个开环反相放大器，具有很高的增益。

这将导致输出电压饱和。随着输入频率的增加，电容器开始充电。在高频下，电容器表现得像短路。

具有直流增益控制的运放积分器​

为了避免输出电压饱和并提供增益控制，可以在反馈电容器 CfC_f 并联一个高阻值电阻。

积分器的闭环增益将是 R2R1\frac{R_2}{R_1}，就像普通的反相放大器一样。

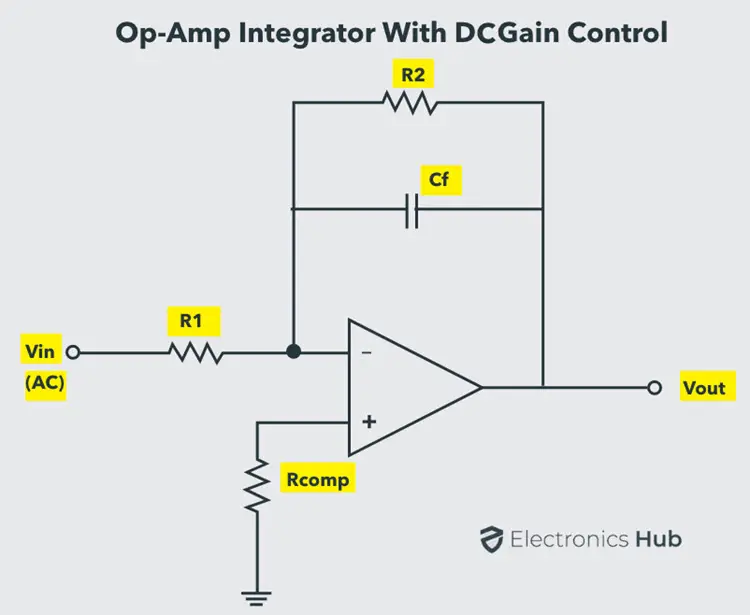
alt text

因此，在输入信号的低频下，电路表现得像一个正常的积分器。在高频下，电容器表现得像短路并绕过反馈电阻 R2R_2。

电容器的阻抗反过来降低了放大器的增益。

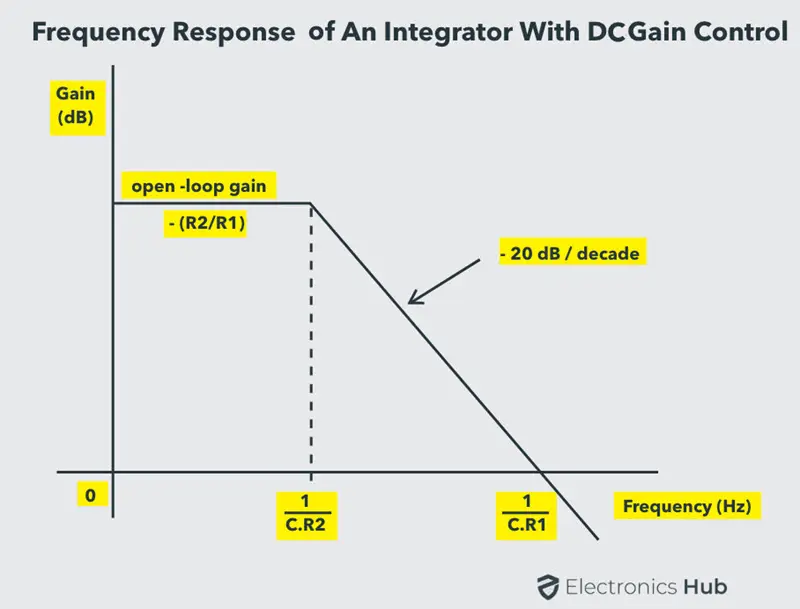
alt text

交流积分放大器的频率响应，具有直流增益控制，如上图所示。在输入信号的低频下，电容器保持未充电状态，表现得像开路。

这导致增益为 R2R1\frac{R_2}{R_1}。随着输入信号频率的增加，反馈电容器开始充电，表现得几乎像短路，绕过反馈电阻 R2R_2。这导致增益以每十倍频程 20 dB 的速率线性下降。

运放积分器的应用​

运放积分放大器用于模拟计算机中执行微积分运算。

积分电路最常用于模数转换器、锯齿波发生器以及波形整形应用。

另一个应用是积分一个代表水流的信号，产生一个代表流过流量计的总水量的信号。在工业仪器领域，这种积分器的应用有时被称为总量计。

运放积分器总结​

运算放大器可用于执行微分和积分等微积分运算。这两种配置都在电路的反馈部分使用了反应元件（通常是电容器而非电感器）。

积分电路对输入信号执行随时间的积分运算，即输出电压与施加的输入电压随时间的积分成正比。

由于输入被施加到运放的反相输入端，积分器的输出与输入相位相差 180°。

积分电路通常用于从方波输入生成锯齿波。积分放大器在处理正弦波信号时存在频率限制。