1.9 巴特沃斯滤波器

巴特沃斯滤波器是一种有源滤波器，其在整个通带内的频率响应相对平坦。由于这种频率响应特性，巴特沃斯滤波器也被称为最大平坦滤波器或平 - 平滤波器。

利用巴特沃斯滤波器技术，可以设计各种类型的滤波器，即高通、低通、带通等。在本教程中，我们将重点介绍使用巴特沃斯滤波器技术设计低通滤波器。

如需了解更多关于典型低通滤波器的信息，无论是有源滤波器还是无源滤波器，请阅读以下教程：无源低通 RC 滤波器和有源低通滤波器。

引言

设计滤波器电路时，主要有以下三个考虑因素：

• 通带的响应必须达到最大平坦度。
• 通带向阻带的过渡必须缓慢。
• 滤波器在通带内无失真地传递信号的能力。

这些失真通常是由波形的相位偏移引起的。除了这三点外，上升时间和下降时间参数也起着重要作用。针对每一种考虑因素，设计出了一种滤波器。

为了实现最大平坦响应，设计了巴特沃斯滤波器。为了实现从通带向阻带的缓慢过渡，设计了切比雪夫滤波器。为了实现最大平坦的时间延迟，设计了贝塞尔滤波器。

巴特沃斯滤波器

巴特沃斯滤波器以牺牲从通带向阻带过渡的陡峭程度为代价，提供了输出信号的平坦响应。因此，它也被称为最大平坦幅度滤波器。

滤波器的衰减响应速率取决于电路中所取的极点数量。极点数量取决于电路中反应元件的数量，即电路中使用的电感或电容的数量。

n 阶巴特沃斯滤波器的幅度响应如下所示：

$\frac{V_{\text{out}}}{V_{\text{in}}} = \frac{1}{\sqrt{1 + \left(\frac{f}{f_c}\right)^{2n}}}$

其中 “n” 为电路中的极点数量。随着 “n” 值的增加，滤波器响应的平坦度也会增加。

“f” = 电路的工作频率，“fc” = 电路的中心频率或截止频率。

这些滤波器具有预先确定的考虑因素，其应用主要在高频有源 RC 电路中。尽管它不能提供锐利的截止响应，但通常被视为一种多功能滤波器，在许多应用中都有使用。

巴特沃斯近似

我们知道，为了满足滤波器响应的考虑因素，并使近似值接近理想滤波器，我们需要使用更高阶的滤波器。这会增加复杂性。

我们也知道低通和高通电路的输出频率响应和相位响应。理想滤波器的特性是最大平坦度、最大通带增益和最大阻带衰减。

为了设计滤波器，需要有适当的传递函数。为了满足这些传递函数，在模拟滤波器设计中进行了许多近似函数的数学推导。

在这些设计中，巴特沃斯滤波器是其中一种滤波器类型。低通巴特沃斯设计考虑因素主要用于许多功能。稍后我们将讨论归一化低通巴特沃斯滤波器多项式。

一阶低通巴特沃斯滤波器

下图展示了一阶低通巴特沃斯滤波器。

巴特沃斯滤波器所需的通带增益主要取决于 “R1” 和 “Rf” 的电阻值，而滤波器的截止频率则取决于上述电路中的 R 和 C 元件。

滤波器的增益为 $A_{\text{max}} = 1 + \frac{R_1}{R_f}$。

电容 “C” 的阻抗由 -jX_C 给出，电容两端的电压为：

$V_c = -\frac{jX_C}{R - jX_C} \times V_{\text{in}}$

其中 $X_C = \frac{1}{2\pi f_c}$，电容抗。

滤波器的传递函数以极坐标形式表示为：

$H(j\omega) = \left|\frac{V_{\text{out}}}{V_{\text{in}}}\right| \angle \phi$

其中滤波器的增益 $\frac{V_{\text{out}}}{V_{\text{in}}} = \frac{A_{\text{max}}}{\sqrt{1 + \left(\frac{f}{f_H}\right)^2}}$。

相位角 $\phi = -\tan^{-1}\left(\frac{f}{f_H}\right)$。

在低频时，即工作频率低于截止频率时，通带增益等于最大增益。

$\frac{V_{\text{out}}}{V_{\text{in}}} = A_{\text{max}} \quad \text{即常数}$

在高频时，即工作频率高于截止频率时，增益小于最大增益。

$\frac{V_{\text{out}}}{V_{\text{in}}} < A_{\text{max}}$

当工作频率等于截止频率时，传递函数等于 $\frac{A_{\text{max}}}{\sqrt{2}}$。增益的下降速率为 -20 dB/十年或 -6 dB/八度，可以表示为响应斜率的 -20 dB/十年。

二阶低通巴特沃斯滤波器

将额外的 RC 网络连接到一阶巴特沃斯滤波器上，就可以得到二阶低通滤波器。这种二阶低通滤波器的一个优势是，在阻带中，截止频率之后增益下降得非常快。

在这种二阶滤波器中，截止频率值取决于两个 RC 部分的电阻和电容值。截止频率的计算公式如下：

$f_c = \frac{1}{2\pi \sqrt{R_2 C_2}}$

增益以 -40 dB/十年的速率下降，这种响应在 -40 dB/十年的斜率中有所体现。滤波器的传递函数可以表示为：

$\frac{V_{\text{out}}}{V_{\text{in}}} = \frac{A_{\text{max}}}{\sqrt{1 + \left(\frac{f}{f_c}\right)^4}}$

二阶滤波器的标准传递函数形式如下：

$\frac{V_{\text{out}}}{V_{\text{in}}} = \frac{A_{\text{max}}}{s^2 + 2\varepsilon \omega_n s + \omega_n^2}$

其中 $\omega_n =$ 自然振荡频率 $= \frac{1}{R_2 C_2}$。

$\varepsilon =$ 阻尼因子 $= \frac{3 - A_{\text{max}}}{2}$。

对于二阶巴特沃斯滤波器，所需的中间项是 $\sqrt{2} = 1.414$，从归一化巴特沃斯多项式中得出：

$3 - A_{\text{max}} = \sqrt{2} = 1.414$

为了确保输出滤波器响应，增益 $A_{\text{max}}$ 必须为 1.586。

更高阶的巴特沃斯滤波器可以通过级联一阶和二阶巴特沃斯滤波器获得。如下所示：

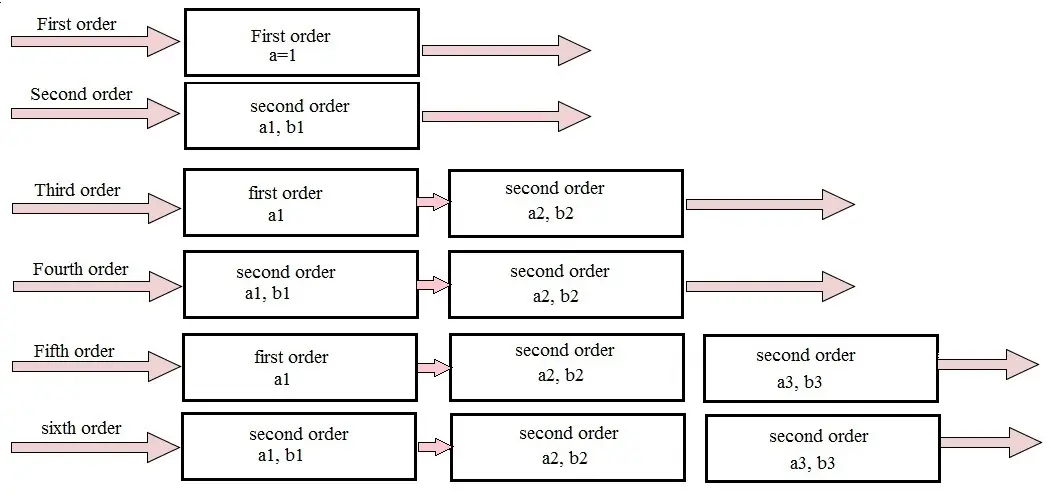
其中 $a_n$ 和 $b_n$ 是预先确定的滤波器系数，这些系数用于生成所需的传递函数。

巴特沃斯滤波器的理想频率响应

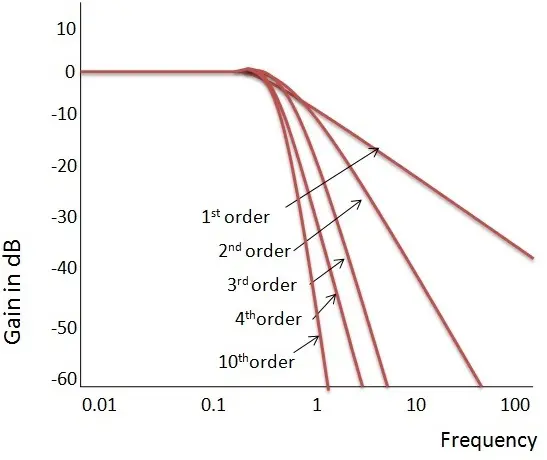
随着滤波器阶数的增加，输出响应的平坦度也会增加。不同阶数的巴特沃斯滤波器的增益和归一化响应如下所示：

归一化低通巴特沃斯滤波器多项式

归一化是一种将电压、电流或阻抗除以相同单位量的过程。这一过程用于创建特定值的无量纲范围或水平。

滤波器传递函数的分母多项式给出了巴特沃斯多项式。如果我们在以原点为中心、半径相等的圆上考虑 s 平面，那么巴特沃斯滤波器的所有极点都位于该 s 平面的左半部分。

对于任何阶数的滤波器，“s” 的最高次幂的系数始终为 1，且任何阶数的滤波器的常数项始终为 1。对于偶数阶滤波器，所有多项式因子均为二次的。对于奇数阶滤波器，除了 1 阶外，所有多项式均为二次的，1 阶滤波器的多项式为 $1+s$ )。

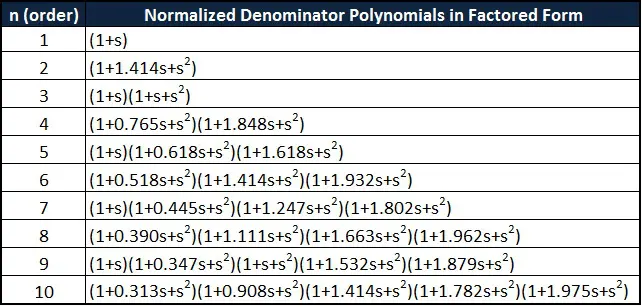
巴特沃斯多项式的系数形式如下表所示：

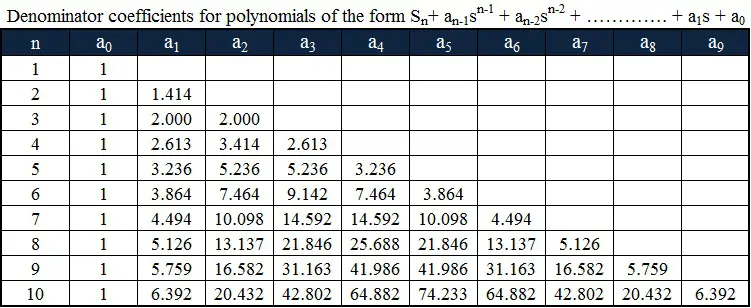
n 阶巴特沃斯滤波器的传递函数如下所示：

$H(j\omega) = \frac{1}{\sqrt{1 + \varepsilon^2 \left(\frac{\omega}{\omega_c}\right)^{2n}}}$

其中 $n$ 是滤波器的阶数，$\omega$ 是角频率，等于 $2\pi f$，而 $\varepsilon$ 是通带最大增益 $A_{\text{max}}$。

巴特沃斯低通滤波器示例

假设一个巴特沃斯低通滤波器的截止频率为 15.9 kHz，通带增益为 1.5，电容 $C = 0.001 \mu\text{F}$。

$f_c = \frac{1}{2\pi RC}$ $15.9 \times 10^3 = \frac{1}{2\pi R_1 \times 0.001 \times 10^{-6}}$ $R = 10 \text{k}\Omega$

假设 $A_{\text{max}} = 1.5$，取 $R_1 = 10 \text{k}\Omega$。

$A_{\text{max}} = 1 + \frac{R_f}{R_1}$ $R_f = 5 \text{k}\Omega$

三阶巴特沃斯低通滤波器

将一阶和二阶巴特沃斯滤波器级联，可以得到三阶巴特沃斯滤波器。三阶巴特沃斯滤波器电路如下图所示：

对于三阶低通滤波器，从给定的归一化低通巴特沃斯多项式中得到的多项式为 $(1+s)(1+s+s^2)$。这个滤波器包含三个未知系数，分别是 $a_0$、$a_1$ 和 $a_2$。

这些系数的值分别为 $a_0 = 1$、$a_1 = 2$ 和 $a_2 = 2$。与一阶滤波器相比，三阶巴特沃斯滤波器的曲线平坦度有所增加。

应用

• 由于其最大平坦通带特性，它被用作数据转换应用中的抗混叠滤波器。

• 它在雷达中有应用，例如在设计雷达目标跟踪显示方面。

• 它在高质量音频应用中被使用。

• 它被用于运动分析的数字滤波器中。