跳到主要内容

1.3 无源高通滤波器

在本教程中，我们将学习无源高通 RC 滤波器，包括其频率响应、无源高通 RC 滤波器的基本电路、应用场景等更多内容。

如需了解无源低通 RC 滤波器的相关信息，请查看这篇教程——无源低通 RC 滤波器。

引言​

电气滤波器是一种电路，用于拒绝电气信号中所有不需要的频率成分，并仅允许所需频率通过。换句话说，滤波器是一种仅允许特定频率范围的电路。

在许多应用中，电容滤波器的使用频率高于电感滤波器，因为电感会产生一些杂散磁场并消耗一定量的功率。这些缺点不仅存在，而且由于电路中使用了电感，滤波器变得笨重。

在前面的教程中，我们已经学习了滤波器的基础知识和无源低通滤波器。现在让我们来看看无源高通 RC 滤波器的工作原理。

无源高通滤波器​

无源高通滤波器与无源低通滤波器类似。当在低通滤波器电路中交换电容和电阻的位置时，电路表现出高通滤波器的特性。电容与电阻串联。输入电压串联施加到电容上，但输出仅在电阻两端取出。

高通滤波器允许高于截止频率 fcf_c 的频率通过，并阻断低频信号。截止频率的值取决于电路设计中所选用的元件值。这些高通滤波器在高达 10 MHz 的高频范围内有许多应用场景。

高通滤波器的电路如下图所示。

alt text

由于电路中元件的这种交换，电容所传递的响应发生了变化，而这些变化与低通滤波器的响应完全相反。

在低频时，电容表现为开路；而在高于截止频率的高频时，电容表现为短路。由于电容的电容抗，电容会阻断进入电容的低频信号。

我们知道，电容本身会阻碍一定量的电流通过，以保持在电容的电容范围内。在截止频率之后，由于电容抗值的减小，电容允许所有频率通过。当输入信号频率大于截止频率 fcf_c 时，电路将整个输入信号传递到输出端。

在低频时，电容抗值增加，因此当电容抗增加时，阻碍电流通过电容的能力也随之增加。低于截止频率的频率范围被称为“阻带”，而高于截止频率的频率范围被称为“通带”。

在上述电路中，仅有一个与电阻配合的反应元件，这表明该电路是一阶电路。

高通滤波器的频率响应​

频率与电容抗的响应曲线如下所示：

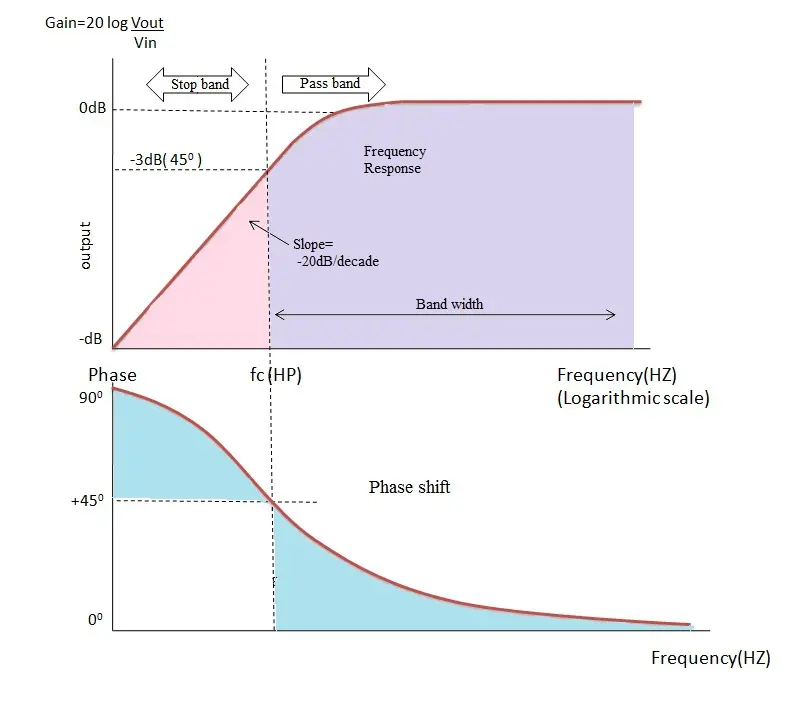
alt text

该响应曲线表明，高通滤波器与低通滤波器完全相反。在高通滤波器中，直到截止频率之前，所有低频信号都被电容阻断，导致输出电压下降。

在截止频率点，电阻 RR 的值与电容的电抗 XCX_C 相等，因此输出电压以 -20 dB/十年的速率增加，输出信号电平比输入信号电平低 -3 dB。

在非常高的频率下，电容抗变为零，此时输出电压与输入电压相同，即 Vout=VinV_{\text{out}} = V_{\text{in}}。在低频时，电容抗为无穷大，因此输出电压为零，因为电容抗会阻断进入电容的电流。

在截止频率时，高通滤波器的输出相对于输入信号具有 +45° 的相位偏移角（ø）。这表明高通滤波器的输出领先于输入信号。在高频（ f>fcf > f_c ）时，相位偏移几乎为零，即输入和输出信号同相。

在理想情况下，滤波器将允许高于截止频率的频率通过，直至无穷大，但在实际应用中，无穷大值取决于滤波器设计中所用的元件值。

电容对输入信号的充放电时间会导致相位差。与电容串联的电阻会产生充放电效应。

串联 RC 电路的时间常数定义为电容充电至最终稳态值的 63.2% 所需的时间，同时也定义为电容放电至稳态值的 36.8% 所需的时间。这用符号 “τ” 表示。时间常数与截止频率之间的关系如下：

τ=RC=12πfc和ωc=1τ=1RC\tau = RC = \frac{1}{2\pi f_c} \quad \text{和} \quad \omega_c = \frac{1}{\tau} = \frac{1}{RC}

由此可以明确，滤波器的输出取决于输入端施加的频率以及时间常数。

截止频率与相位偏移​

截止频率或转折点 fcf_c：

fc=12πRCf_c = \frac{1}{2\pi RC}

相位偏移（ø）：

ϕ=tan⁡−1(2πfRC)\phi = \tan^{-1}(2\pi fRC)

高通 RC 滤波器的输出电压与增益​

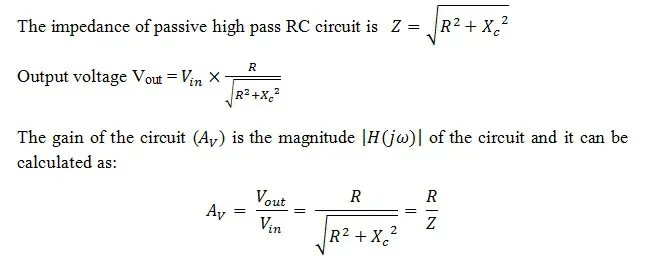
alt text

高通滤波器示例​

假设一个高通滤波器的电容值为 82 pF，电阻值为 240 kΩ。根据这些值，我们来计算滤波器的截止频率：

fc=12πRC=12π×240×103×82×10−12≈8.08 kHzf_c = \frac{1}{2\pi RC} = \frac{1}{2\pi \times 240 \times 10^3 \times 82 \times 10^{-12}} \approx 8.08 \text{ kHz}

二阶无源高通滤波器​

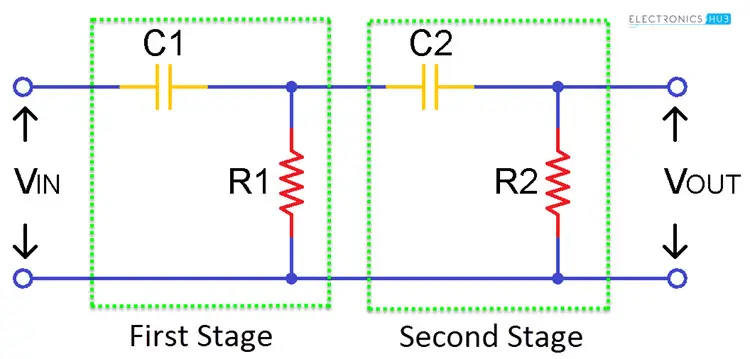
alt text

通过级联两个一阶高通滤波器，我们可以得到二阶高通滤波器。由于它包含两个反应元件（即两个电容），因此该电路为二阶电路。这种双级滤波器的性能等同于单级滤波器，但滤波器的斜率在 -40 dB/十年处获得。

这是由于截止频率的变化。与单级高通滤波器相比，它更高效，因为它有两个存储点。对于两级滤波器，截止频率取决于两个电容和两个电阻的值。计算公式如下：

fc=12πR1C1R2C2 Hzf_c = \frac{1}{2\pi \sqrt{R_1C_1R_2C_2}} \text{ Hz}

无源高通滤波器总结​

高通滤波器允许从截止频率到无穷大的频率通过。在实际情况下，无穷大并不存在，因此这个无穷大值取决于电路设计中所用的元件。

高通滤波器所允许的频率范围被称为“通带”，而通带实际上就是滤波器的带宽。滤波器所衰减的频率范围被称为“阻带”。

截止频率可以通过上述公式 fcf_c 计算得出。输出信号的相位偏移领先于输入信号 +45°。输出电压取决于电路的时间常数以及施加的输入频率。

与低通滤波器相比，高通滤波器所消除的失真更为准确，原因在于电路中使用了高频信号。

高通 RC 微分器​

对于普通的正弦波输入，滤波器的性能就像一阶高通滤波器一样。但是，当我们施加非正弦波信号（如方波）时，这些信号在时域中的响应表现为阶跃或脉冲输入信号，此时电路表现为微分器电路。

如果一个电路的输入导数与电路的输出成正比，则该电路被称为微分器电路。

alt text

因此，当向电路施加恒定输入时，输出变为零，因为常数的导数趋于零。

RC 微分电路如下图所示：

alt text

对于方波输入信号，输出波形表现为短时脉冲。在输入信号的一个完整周期内，会出现两个尖峰信号，分别带有正脉冲和负脉冲。

在这个过程中，输出信号的幅度不会发生变化。如果输入信号频率增加，那么输出脉冲的宽度也会增加。尖峰脉冲的衰减速率取决于时间常数。

高通滤波器的应用​

  • 这些滤波器被用于音频放大器电路中，作为高音频分频器的一部分，用于传递高频信号（如高音喇叭信号），同时阻断低频信号。
  • 这些滤波器被用作低频滤波器，以阻断附近不需要的信号，并在扬声器中传递所需的信号。
  • 这些滤波器被用于交流耦合电路以及微分器电路。
  • 在每个声道条的混音过程中，都会添加这些高通滤波器。
  • 在图像处理中，高通滤波器被用于锐化处理