1.2 无源低通滤波器
在本教程中,我们将学习无源低通 RC 滤波器。顾名思义,这是一种使用无源元件设计的低通滤波器。在以下各节中,您可以了解无源低通 RC 滤波器的基本电路、频率响应、输出电压、应用场景等更多信息。
如需了解无源高通 RC 滤波器的相关信息,请阅读“无源高通 RC 滤波器”教程。
滤波器是一种用于筛选信号的电路,即它仅允许所需的信号通过,而避免不需要的信号。通常,滤波器由无源元件或有源元件设计而成。
- 无源元件包括电阻、电感和电容。
- 有源元件包括晶体管、场效应晶体管和运算放大器。
低通滤波器是一种仅允许低频信号通过并衰减或阻止高频信号的滤波器。它仅允许从 0 Hz 到截止频率 的信号通过。截止频率的值取决于电路中所用元件的值。
通常,这些滤波器适用于频率低于 100 kHz 的场景。截止频率也被称为转折频率或转折频率。
无源低通滤波器
使用无源元件设计的低通滤波器被称为无源低通滤波器。
以下图展示了一个简单的 RC 低通滤波器电路。
仅通过将电阻 与电容 串联即可构成 RC 低通滤波器。它也可以简单地被称为低通滤波器(LPF)。电阻对电路中施加频率的变化不敏感,但电容是一种敏感元件,即它会对电路中的变化做出响应。
由于该电路仅包含一个反应元件,因此也可以被称为“单极滤波器”或“一阶滤波器”。输入电压 串联施加到电阻上,而输出电压仅在电容两端取出。
由于电容是一种敏感元件,因此需要关注“电容抗”。电容抗是由于电路中的电容而产生的阻抗响应。
为了维持电容的电容值,电容会对电路中的电流流动产生一定的阻碍。这种对电路中电流流动的阻碍被称为阻抗。因此,随着阻碍电流的增加,电容抗会减小。
由此可以得出,电容抗与施加到电路中的频率成反比。电阻的阻值是稳定的,而电容抗的值是变化的。电容两端的电压降与电容的电位相比非常小。
这意味着在低频时,电压降较小,而电位较大;但在高频时,电压降非常高,而电位较小。通过这种现象,我们可以得出上述电路可以作为一个“频率可变的电压分配器”电路。
电容抗的计算公式如下:
输出电压计算
为了得到电位分配器方程,我们需要考虑阻抗、电容抗、输入电压和输出电压。利用这些参数,我们可以推导出 RC 电位分配器方程,如下所示:
利用该方程,我们可以计算在任何施加频率下的输出值。
低通滤波器示例
让我们通过考虑电阻和电容的值来检验这些输出电压值和电容抗值。假设电阻 的值为 4.7 kΩ,电容值为 47 nF。施加的交流输入电压为 10 V。我们将要计算的频率值分别为 1 kHz 和 10 kHz。
当频率增加时,电容抗减小。不仅电容抗减小,输出电压也随之减小。
从上述示例可以看出,电容抗从 3386.27 Ω 降至 338.62 Ω,而输出电压从 5.84 V 降至 0.718 V,频率从 1 kHz 增加到 10 kHz。
低通滤波器的频率响应
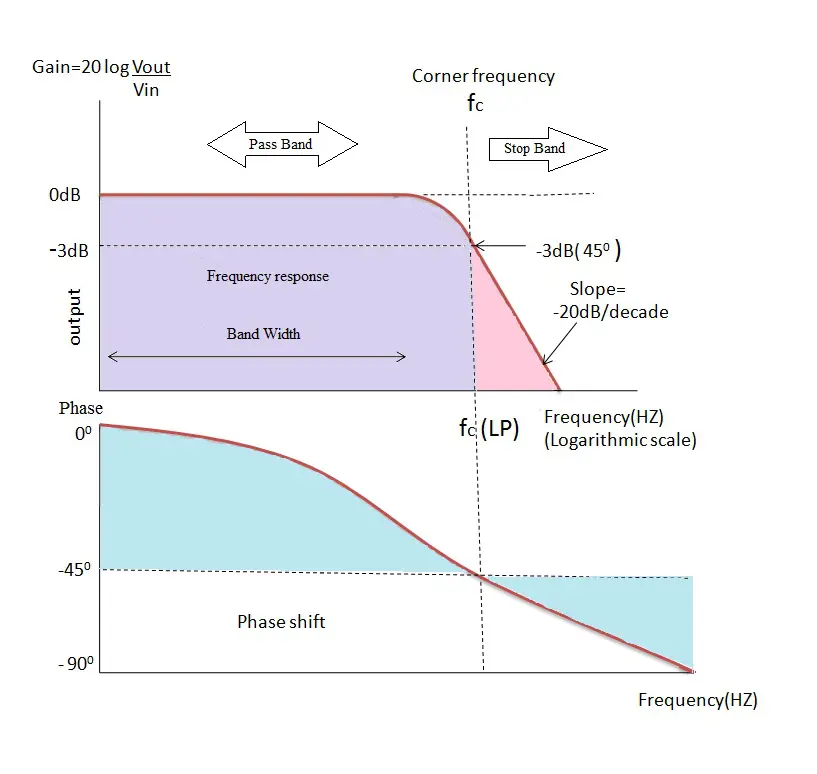
从滤波器的介绍中我们已经了解到,滤波器的幅度 被视为电路的增益。该增益以 表示,对于任何 RC 电路,其“滚降”角度的斜率为 -20 dB/十年,这是相同的。
低于截止区域的频率范围被称为“通带”,而截止频率之后的频率范围被称为“阻带”。从曲线图中可以观察到,通带是滤波器的带宽。
从该曲线图可以清楚地看出,直到截止频率为止,增益保持不变,因为输出电压与低频时的频率值成正比。这是由于电容抗在低频时像开路一样,允许电路中通过最大电流,而在高频时则不然。低频时电容抗的值非常高,因此其阻止电流通过电路的能力更强。
一旦达到截止频率值,输出电压会逐渐减小并趋于零。增益也会随着输出电压的减小而减小。在截止频率之后,电路响应的斜率会达到滚降点,该点出现在 -20 dB/十年。
这主要是由于频率的增加,当频率增加时,电容抗值减小,从而通过电容的电流阻断能力降低。当电路中的电流增加且由于电容的有限电容值,电路表现为短路。因此,在高频时滤波器的输出电压为零。
避免这一问题的唯一方法是选择这些电阻和电容能够承受的频率范围。电容和电阻的值起着主要作用,因为截止频率 仅取决于这些值。如果频率范围在截止频率范围内,则可以克服短路问题。
当电阻值和电容抗值相同时,会出现截止点,即电阻和电容抗的向量和相等。在这种情况下,输入信号被衰减 -3 dB/十年。这种衰减约为输入信号的 70.7%。电容极板的充电和放电时间会根据正弦波的变化而变化。因此,输出信号的相位角(ø)在截止频率之后会滞后于输入信号。在截止频率时,输出信号的相位滞后 -45°。
如果滤波器的输入频率增加,电路输出信号的滞后角会增大。简单来说,频率越高,电路的相位差越大。
在低频时,电容有更多的时间对极板进行充电和放电,因为正弦波的切换时间更长。但随着频率的增加,切换到下一个脉冲所需的时间逐渐减少。由于此原因,时间变化会导致输出波的相位偏移。
无源低通滤波器的截止频率主要取决于滤波器电路中所用电阻和电容的值。截止频率与电阻和电容值成反比。无源低通滤波器的截止频率计算公式为:
无源低通滤波器的相位偏移计算公式为:
时间常数(τ)
正如我们已经看到的那样,电容对输入正弦波的极板充电和放电所需的时间会导致相位差。串联连接的电阻和电容会产生这种充电和放电效应。
串联 RC 电路的时间常数定义为电容充电至最终稳态值的 63.2% 所需的时间,同时也定义为��电容放电至稳态值的 36.8% 所需的时间。该时间常数用符号 “τ” 表示。
时间常数与截止频率之间的关系如下:
我们也可以用截止频率来表示:
由此我们可以得出,滤波器的输出取决于输入端施加的频率以及时间常数。
无源低通滤波器示例 2
让我们计算一个具有 4.7 kΩ 电阻和 47 nF 电容的低通滤波器的截止频率。
我们知道截止频率的公式为:
二阶无源低通滤波器
到目前为止,我们已经研究�了一阶低通滤波器,它是通过将电阻和电容串联而成的。然而,有时单个阶段可能不足以去除所有不需要的频率,因此会使用二阶滤波器,如下图所示。
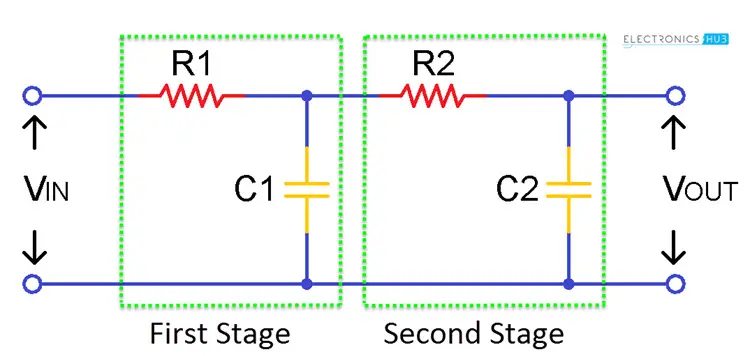
二阶低通 RC 滤波器可以通过在一阶低通滤波器的基础上再增加一个阶段来简单地实现。这种滤波器的斜率为 -40 dB/十年或 -12 dB/八度,而四阶滤波器的斜率为 -80 dB/八度,依此类推。
无源低通滤波器在截止频率处的增益为
其中 为滤波器的阶数或级数。
二阶低通滤波器的截止频率为
二阶低通滤波器的 -3 dB 频率为
其中 为截止频率, 为级数, 为 -3 dB 通带频率。
低通滤波器总结
低通滤波器由电阻和电容组成。不仅是电容,任何与电阻配合的反应元件都可以构成低通滤波器。它是一种仅允许低频信号通过并衰减高频信号的滤波器。
低于截止频率的频率称为通带频率,而高于截止频率的频率称为阻带频率。通带即为滤波器的带宽。
滤波器的截止频率取决于电路设计中所选用的元件值。截止频率可以通过以下公式计算得出:
滤波器的增益以滤波器的幅度来衡量,增益可通过以下公式计算:
在频率达到截止频率之前,滤波器的输出保持不变。
在截止频率时,输出信号为输入信号的 70.7%,而在截止频率之后,输出逐渐减小至零。截止频率之后,输出信号的相位角滞后于输入信号。
在截止频率时,输出信号的��相位偏移为 45°。
如果我们在低通滤波器电路中交换电阻和电容的位置,那么电路将表现为高通滤波器。
对于正弦波输入,电路表现为一阶低通滤波器。我们已经研究过一阶滤波器的工作原理,但如果输入信号类型发生变化,那么滤波器的输出会发生什么变化需要进行观察。
当我们将输入信号类型改为开关模式(开/关)或方波时,电路将表现为积分器,相关内容如下所述。
低通滤波器作为波形整形电路
上图展示了滤波器对方波输入的性能表现。当低通滤波器的输入为方波时,滤波器的输出将呈现三角波形。
这是因为电容无法作为开关来实现开或关的操作。当输入为方波且频率较低时,滤波器的输出也将是方波。
当频率增加时,滤波器的输出看起来像三角波。如果继续增加频率,输出信号的幅度会减小。
三角波的产生是由于电容的作用,或者更简单地说,电容的充放电模式导致了三角波的形成。
低通滤波器的应用
- 低通滤波器电路的主要用途是避免整流器输出中的交流纹波。低通滤波器用于音频放大器电路。
- 通过使用这种无源低通滤波器,我们可以直接将高频噪声降低到立体声系统中的小干扰模式。
- 低通滤波器作为积分器,可用于波形整形和波形生成电路,因为可以轻松地将一种类型的电信号转换为另一种形式。
- 它们还用于解调器电路,以从调制信号中提取所需的参数。