1.9 复用器

想象一下，将高清视频、音乐、电子邮件、电话通话和互联网数据全部通过一根电线传输！这就是多路复用的“魔法”，而多路复用器（简称 MUX）则是实现这一功能的“小巫师”。在本指南中，您将了解什么是多路复用器，不同类型的多路复用器（如 2 到 1、4 到 1、8 到 1 和 16 到 1 多路复用器），常见的多路复用器集成电路（IC），以及多路复用器的一些重要应用。

多路复用是什么？

多路复用是将一个或多个信号组合起来并在单一信道上传输的过程。在模拟通信系统中，通信信道是一种稀缺资源，必须合理利用。为了以成本效益高且高效的方式使用信道，多路复用的概念非常有用，因为它允许多个用户以合理的方式共享单一信道。

常见的三种多路复用方法是：

• 时间
• 频率
• 空间

我们在日常生活中使用的两个最佳多路复用系统示例是固定电话网络和有线电视。

负责多路复用的设备被称为多路复用器。多路复用器既用于模拟信号，也用于数字信号。在本教程中，我们专注于数字信号，以保持内容简洁。多路复用器是最常用的组合逻辑电路之一，也是许多数字系统的重要构建模块。

它们主要用于在多个源和单一目的地之间形成选定的路径。基本的多路复用器有多个数据输入线和一个输出线。它们在许多数字系统应用中都有使用，例如数据选择和数据路由、逻辑函数发生器、带有复用显示器的数字计数器、电话网络、通信系统、波形发生器等。在本文中，我们将讨论多路复用器的类型及其设计。

什么是多路复用器？

多路复用器（MUX）是一种数字开关，也被称为数据选择器。它是一种具有多个输入线、一个输出线和多个选择线的组合逻辑电路。它从多个输入线或源接收二进制信息，并根据选择线的组合，将特定的输入线路由到单一输出线。

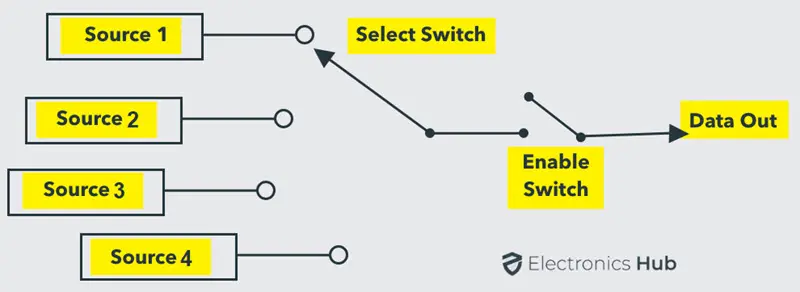
多路复用的基本原理如下图所示，当使能开关处于打开状态时，来自多个源的数据被路由到单一输出线。这就是为什么多路复用器也被称为“多对一”组合电路。

下图展示了一个多路复用器的框图，包含 $n$ 个输入线、$m$ 个选择线和一个输出线。如果有 $m$ 个选择线，则可能的输入线数量为 $2^m$。反之，如果输入线的数量为 $2^m$，则需要 $m$ 个选择线来选择 $n$ 条输入线中的某一条（假设 $2^m = n$）。

这种类型的多路复用器被称为 $2^n \times 1$ 多路复用器或 $2^n$-to-1 多路复用器。例如，如果输入线的数量为 4，则需要两条选择线。同样，为了选择 8 条输入线中的某一条，需要三条选择线。

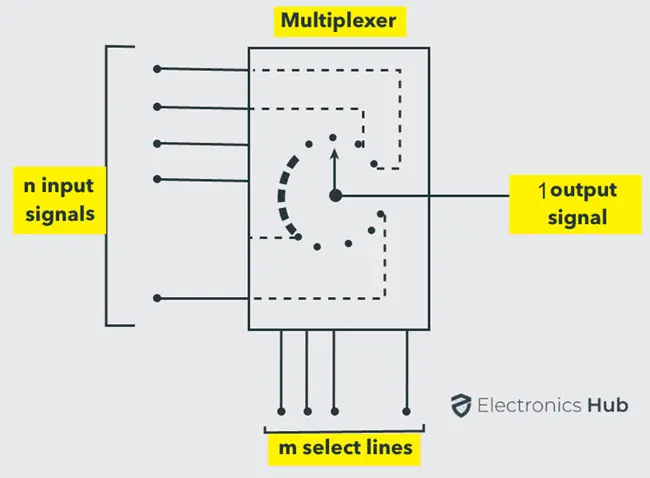
通常，多路复用器的数据输入数量是 2 的幂，例如 2、4、8、16 等。一些最常用的多路复用器包括 2-to-1、4-to-1、8-to-1 和 16-to-1 多路复用器。

这些多路复用器以集成电路（IC）的形式存在，具有不同的输入和选择线配置。一些常见的多路复用器 IC 包括 74157（四通道 2-to-1 MUX）、78158（带反相输出的四通道 2-to-1 MUX）、74153（4-to-1 MUX）、74152（8-to-1 MUX）和 74150（16-to-1 MUX）。

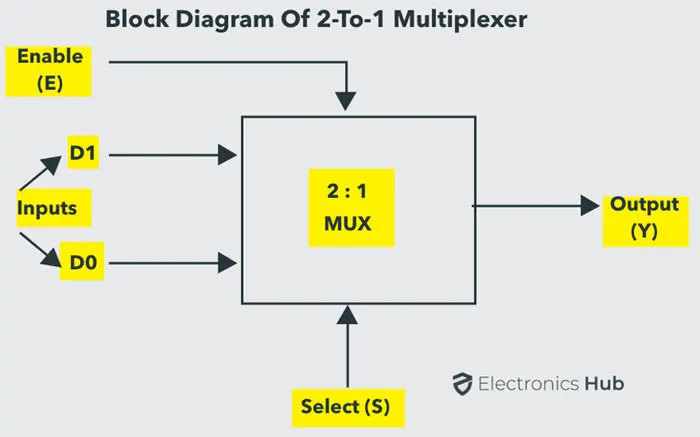
2 到 1 多路复用器

2 到 1 多路复用器包含两个输入 $D_0$ 和 $D_1$、一个选择输入 $S$ 和一个输出 $Y$。根据选择信号，输出连接到其中一个输入。由于有两个输入信号，因此只有两种可能的方式将输入连接到输出，因此需要一个选择信号来执行这些操作。

如果选择线为低电平，则输出将切换到 $D_0$ 输入；如果选择线为高电平，则输出将切换到 $D_1$ 输入。下图展示了 2:1 多路复用器的框图，它将两个 1 位输入连接到一个公共目的地。

2×1 多路复用器计算器

2 到 1 多路复用器的真值表如下所示。根据选择输入的值，输入 $D_0$ 和 $D_1$ 会在输出处产生。当选择值 $S = 0$ 时，输出为 $D_0$；当选择值 $S = 1$ 时，输出为 $D_1$。

S	D0	D1	Y
0	0	X	0
0	1	X	1
1	X	0	0
1	X	1	1

在上述 2:1 多路复用器的真值表中，“X”表示“不关心”条件。因此，忽略“不关心”条件，我们可以得出典型的 2:1 多路复用器的布尔表达式如下：

$Y = \overline{S} D_0 + S D_1$

根据上述输出表达式，可以使用逻辑门实现 2-to-1 多路复用器的逻辑电路，如下图所示。它包含两个与门、一个非门和一个或门。当选择线 $S = 0$ 时，下部与门的输出为零，而上部与门的输出为 $D_0$。因此，由或门产生的输出等于 $D_0$。

同样，当 $S = 1$ 时，上部与门的输出为零，而下部与门的输出为 $D_1$。因此，或门的输出为 $D_1$。因此，上述给定的多路复用器布尔表达式被该电路满足。

为了高效利用硅片，集成电路制造商通常会在单个集成电路中制造多个多路复用器。通常，单个集成电路中会制造四个 2 线到 1 线的多路复用器。一些常见的 2 到 1 多路复用器集成电路包括 74157 和 74158。

这两种集成电路都是四通道 2-to-1 多路复用器。74157 集成电路具有正常输出，而 74158 集成电路具有反相输出。只有一个选择线，用于控制所有四个多路复用器的输入到输出。输出 $Y_0$ 可以是 $A_0$ 或 $B_0$，具体取决于选择线的状态。同样，$Y_1$ 可以是 $A_1$ 或 $B_1$，$Y_2$ 可以是 $A_2$ 或 $B_2$，依此类推。还有一个额外的使能控制输入 $E$ / Strobe，用于启用或禁用所有多路复用器，即当 $E = 1$ 时，无论 $S$ 的值如何，所有多路复用器的输出均为零。

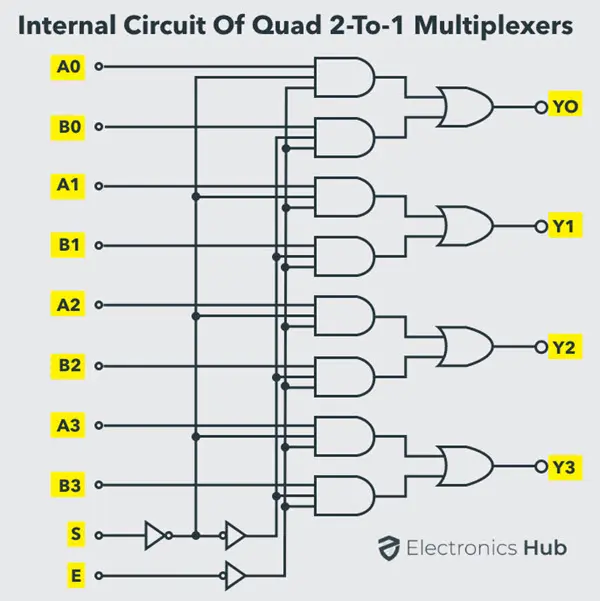
所有多路复用器仅在 $E$ / Strobe 输入为低电平时才被激活。

4 到 1 多路复用器

4 到 1 多路复用器包含四个数据输入线 $D_0$ 到 $D_3$、两个选择线 $S_0$ 和 $S_1$ 以及一个输出线 $Y$。选择线 $S_0$ 和 $S_1$ 用于选择四个输入线中的某一条以连接到输出线。下图展示了 4:1 多路复用器的框图，其中，多路复用器通过选择线对输入进行解码。

4×1 多路复用器计算器

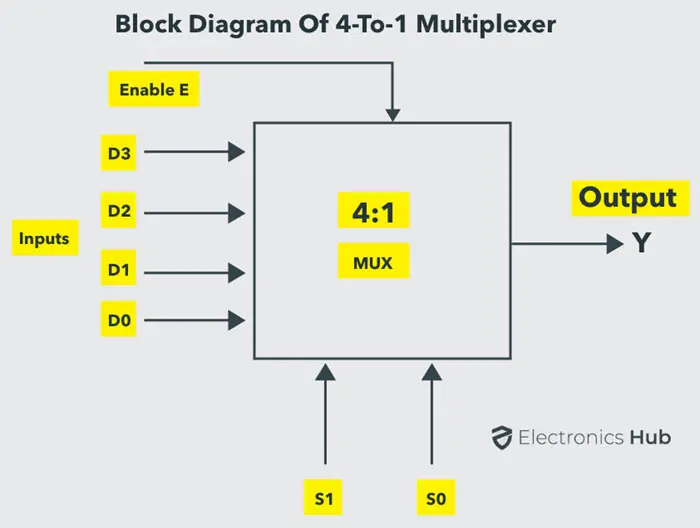
4×1 多路复用器的真值表如下所示，其中选择线上的四种输入组合 00、10、01 和 11 分别将输入 $D_0$、$D_2$、$D_1$ 和 $D_3$ 切换到输出。也就是说，当 $S_0 = 0$ 且 $S_1 = 0$ 时，输出 $Y$ 为 $D_0$；同样，如果选择输入 $S_0 = 0$ 且 $S_1 = 1$，则输出 $Y$ 为 $D_1$，依此类推。

$S_0$	$S_1$	$D_0$	$D_1$	$D_2$	$D_3$	$Y$
0	0	0	X	X	X	0
0	0	1	X	X	X	1
0	1	X	0	X	X	0
0	1	X	1	X	X	1
1	0	X	X	0	X	0
1	0	X	X	1	X	1
1	1	X	X	X	0	0
1	1	X	X	X	1	1

从上述 4:1 多路复用器真值表中，我们可以写出输出表达式如下：

$Y = \overline{S_0} \overline{S_1} D_0 + \overline{S_0} S_1 D_1 + S_0 \overline{S_1} D_2 + S_0 S_1 D_3$

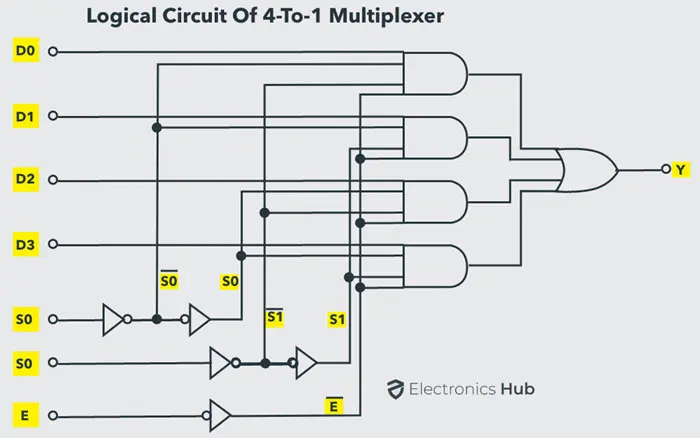
根据上述输出表达式，可以使用基本逻辑门实现 4-to-1 多路复用器。下图展示了 4:1 MUX 的逻辑电路，它由四个 3 输入与门、两个 1 输入非门和一个 4 输入或门实现。

在这个电路中，每个数据输入线连接到一个与门的输入端，而两个选择线连接到该与门的另外两个输入端。此外，还有一个使能信号。所有与门的输出连接到或门的输入端，以产生输出 $Y$。

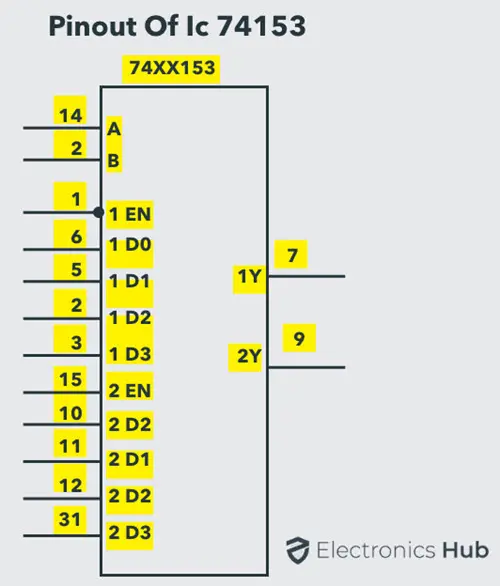
通常，这种类型的多路复用器以双模式集成电路（IC）的形式存在，即在一个集成电路中有两个 4-to-1 多路复用器。最常见和流行的 4-to-1 线多路复用器是 IC 74153，它是一个双 4-to-1 线多路复用器。它包含两个相同的 4-to-1 多路复用器。它有两个独立的使能或选通信号输入，用于打开或关闭各个多路复用器。但选择线对两个多路复用器是共用的。

通常，使能输入或选通可以用于级联两个或多个多路复用器集成电路，以构建具有大量输入的多路复用器。每个乘法器都提供独立的输入。下图展示了 IC74153 的引脚图。

8 到 1 多路复用器

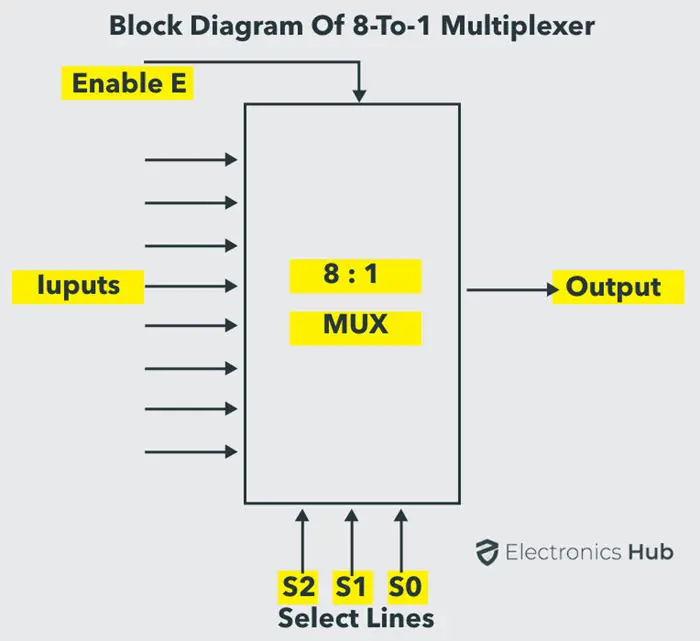
8 到 1 多路复用器包含八个数据输入 $D_0$ 到 $D_7$、三个输入选择线 $S_0$ 到 $S_2$ 以及一个输出线 $Y$。根据选择线的组合，多路复用器选择输入。

下图展示了带有使能输入的 8-to-1 多路复用器的框图，该使能输入可以启用或禁用多路复用器。由于提供给 MUX 的数据位数为八，因此需要 3 位（$2^3 = 8$）来选择八个数据位中的一个。

8×1 多路复用器计算器

8 到 1 多路复用器的真值表如下所示，其中包含八种输入组合，以便生成每个输出对应于输入。

例如，如果 $S_2 = 0$、$S_1 = 1$ 且 $S_0 = 0$，则数据输出 $Y$ 等于 $D_2$。同样，数据输出 $D_0$ 到 $D_7$ 将通过 $S_2$、$S_1$ 和 $S_0$ 的组合进行选择，如下图所示。

$S_0$	$S_1$	$S_2$	$D_0$	$D_1$	$D_2$	$D_3$	$D_4$	$D_5$	$D_6$	$D_7$	$Y$
0	0	0	0	X	X	X	X	X	X	X	0
0	0	0	1	X	X	X	X	X	X	X	1
0	0	1	X	0	X	X	X	X	X	X	0
0	0	1	X	1	X	X	X	X	X	X	1
0	1	0	X	X	0	X	X	X	X	X	0
0	1	0	X	X	1	X	X	X	X	X	1
0	1	1	X	X	X	0	X	X	X	X	0
0	1	1	X	X	X	1	X	X	X	X	1
1	0	0	X	X	X	X	0	X	X	X	0
1	0	0	X	X	X	X	1	X	X	X	1
1	0	1	X	X	X	X	X	0	X	X	0
1	0	1	X	X	X	X	X	1	X	X	1
1	1	0	X	X	X	X	X	X	0	X	0
1	1	0	X	X	X	X	X	X	1	X	1
1	1	1	X	X	X	X	X	X	X	0	0
1	1	1	X	X	X	X	X	X	X	1	1

从上述8:1多路复用器的真值表中，输出的布尔方程为：

$Y = \overline{S_0}\overline{S_1}\overline{S_2} D_0 + \overline{S_0} \overline{S_1} S_2 D_1 + \overline{S_0} S_1 \overline{S_2} D_2 + \overline{S_0} S_1 S_2 D_3 + S_0 \overline{S_1} \overline{S_2} D_4 + S_0 \overline{S_1} S_2 D_5 + S_0 S_1 \overline{S_2} D_6 + S_0 S_1 S_2 D_7$

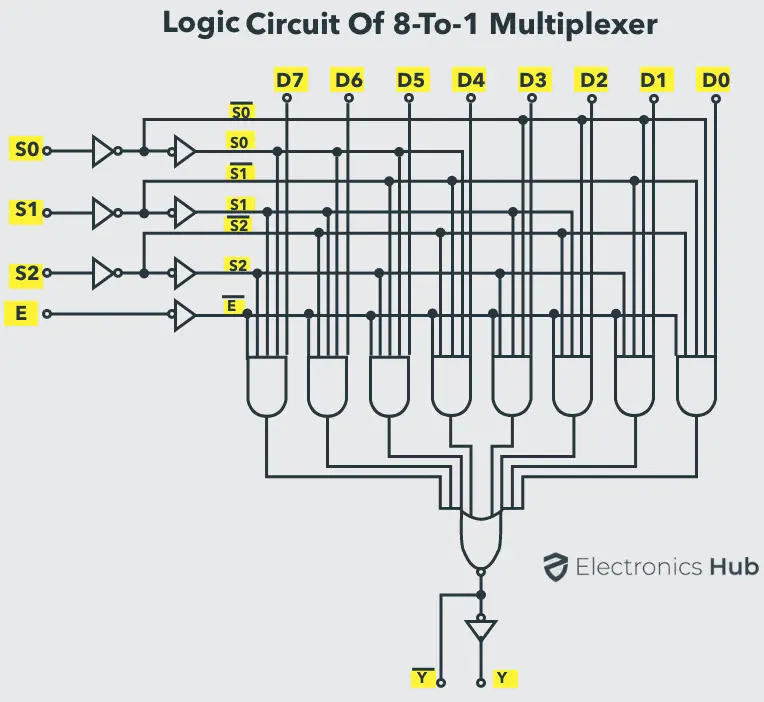
根据上述布尔方程，可以使用8个与门、1个或门和7个非门实现8-to-1多路复用器的逻辑电路，如下图所示。在该电路中，当使能引脚设置为1时，多路复用器将被禁用；如果为0，则选择线将选择相应的数据输入以通过输出。

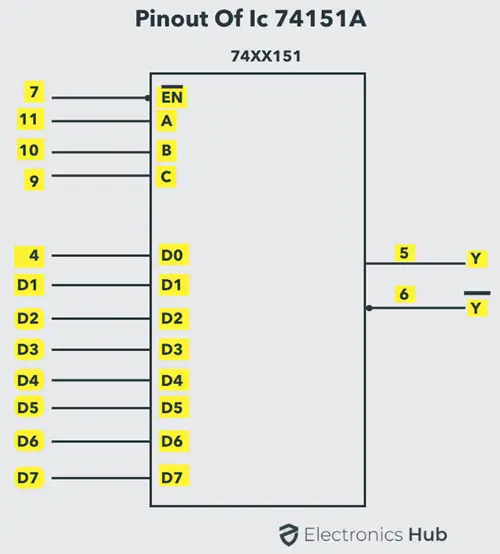
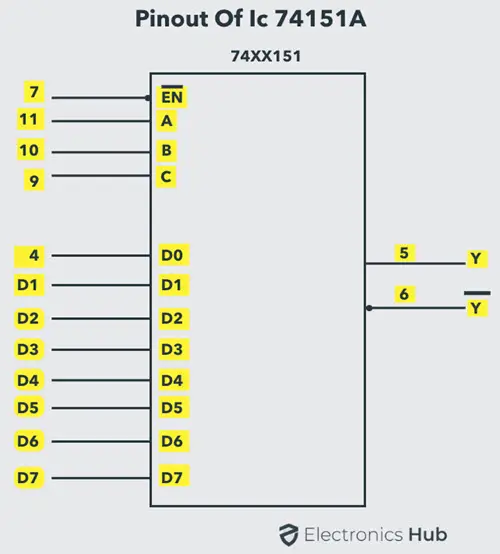
IC 74151是一种流行的8-to-1多路复用器IC，具有八个输入和两个输出。这两个输出是低电平有效和高电平有效的输出。它有三个选择线A、B和C以及一个低电平有效的使能输入。该IC的引脚图如下所示。

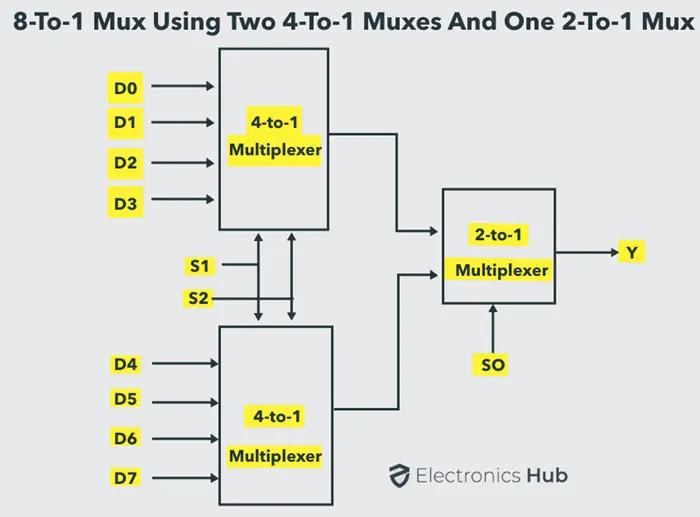
使用4到1多路复用器和2到1多路复用器实现8到1多路复用器

如果你观察上述8-to-1多路复用器的布尔表达式，我们可以将其重写如下：

$Y = \overline{S_0} \overline{S_1} \overline{S_2} D_0 + \overline{S_0} \overline{S_1} S_2 D_1 + \overline{S_0} S_1 \overline{S_2} D_2 + \overline{S_0} S_1 S_2 D_3 + S_0 \overline{S_1} \overline{S_2} D_4 + S_0 \overline{S_1} S_2 D_5 + S_0 S_1 \overline{S_2} D_6 + S_0 S_1 S_2 D_7$ $Y = \overline{S_0} (\overline{S_1} \overline{S_2} D_0 + \overline{S_1} S_2 D_1 + S_1 \overline{S_2} D_2 + S_1 S_2 D_3) + S_0(\overline{S_1} \overline{S_2} D_4 + \overline{S_1} S_2 D_5 + S_1 \overline{S_2} D_6 + S_1 S_2 D_7)$

第一个括号内的表达式 $\overline{S_1} \overline{S_2} D_0 + \overline{S_1} S_2 D_1 + S_1 \overline{S_2} D_2 + S_1 S_2 D_3$ 与4-to-1多路复用器的布尔表达式相似，其输入为 $D_0, D_1, D_2, D_3$，选择线为 $S_1, S_2$。设此表达式为 $P_1$。

同样，第二个括号内的表达式 $\overline{S_1} \overline{S_2} D_4 + \overline{S_1} S_2 D_5 + S_1 \overline{S_2} D_6 + S_1 S_2 D_7$ 与另一个4-to-1多路复用器的布尔表达式相似，其输入为 $D_4, D_5, D_6, D_7$，选择线为 $S_1, S_2$。设此表达式为 $P_2$。

现在，用 $P_1$ 和 $P_2$ 替换上述表达式，我们得到：

$\overline{S_0} P_1 + S_0 P_2$

这个表达式类似于2-to-1多路复用器，其输入为 $P_1$ 和 $P_2$（其中 $P_1$ 和 $P_2$ 分别是相应4-to-1多路复用器的输出），选择信号为 $S_0$。因此，最终我们可以推断出，8-to-1多路复用器可以使用两个4-to-1多路复用器和一个2-to-1多路复用器来实现。其框图如下所示：

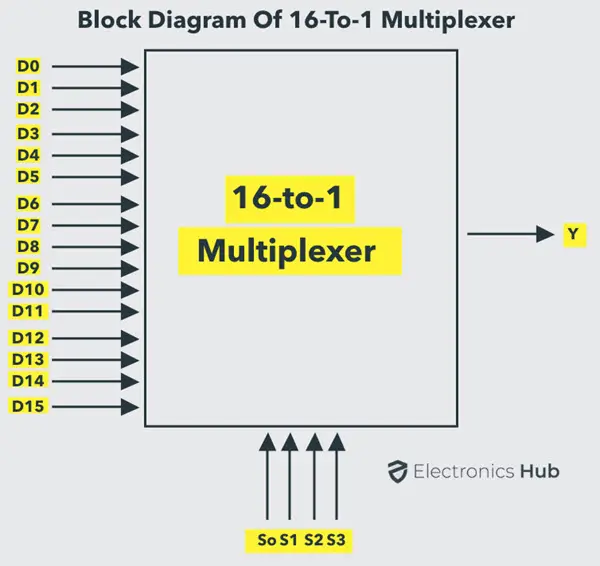
16到1多路复用器

所有高阶多路复用器，如8-to-1、16-to-1等，都可以使用低阶多路复用器来实现。但无论如何，让我们快速了解一下16-to-1多路复用器。IC 74150是一种流行的16-to-1多路复用器IC。16:1多路复用器的输入为 $D_0, D_1, D_2, \ldots, D_{15}$。由于它有16个输入线，因此将有4个选择线，分别为 $S_0, S_1, S_2, S_3$。

下图展示了一个典型的16到1多路复用器的框图。

16×1多路复用器的简化真值表如下表所示。

$S_0$	$S_1$	$S_2$	$S_3$	$Y$
0	0	0	0	$D_0$
0	0	0	1	$D_1$
0	0	1	0	$D_2$
0	0	1	1	$D_3$
0	1	0	0	$D_4$
0	1	0	1	$D_5$
0	1	1	0	$D_6$
0	1	1	1	$D_7$
1	0	0	0	$D_8$
1	0	0	1	$D_9$
1	0	1	0	$D_{10}$
1	0	1	1	$D_{11}$
1	1	0	0	$D_{12}$
1	1	0	1	$D_{13}$
1	1	1	0	$D_{14}$
1	1	1	1	$D_{15}$

16-to-1多路复用器的布尔表达式如下：

16 到 1 多路复用器的布尔方程

16 到 1 多路复用器的布尔方程如下：

$Y = \overline{S_0} \overline{S_1} \overline{S_2} \overline{S_3} D_0 + \overline{S_0} \overline{S_1} \overline{S_2} S_3 D_1 + \overline{S_0} \overline{S_1} S_2 \overline{S_3} D_2 + \overline{S_0} \overline{S_1} S_2 S_3 D_3 + \overline{S_0} S_1 \overline{S_2} \overline{S_3} D_4 + \overline{S_0} S_1 \overline{S_2} S_3 D_5 + \overline{S_0} S_1 S_2 \overline{S_3} D_6 + \overline{S_0} S_1 S_2 S_3 D_7 + S_0 \overline{S_1} \overline{S_2} \overline{S_3} D_8 + S_0 \overline{S_1} \overline{S_2} S_3 D_9 + S_0 \overline{S_1} S_2 \overline{S_3} D_{10} + S_0 \overline{S_1} S_2 S_3 D_{11} + S_0 S_1 \overline{S_2} \overline{S_3} D_{12} + S_0 S_1 \overline{S_2} S_3 D_{13} + S_0 S_1 S_2 \overline{S_3} D_{14} + S_0 S_1 S_2 S_3 D_{15}$

下图展示了 16 到 1 多路复用器的逻辑电路。

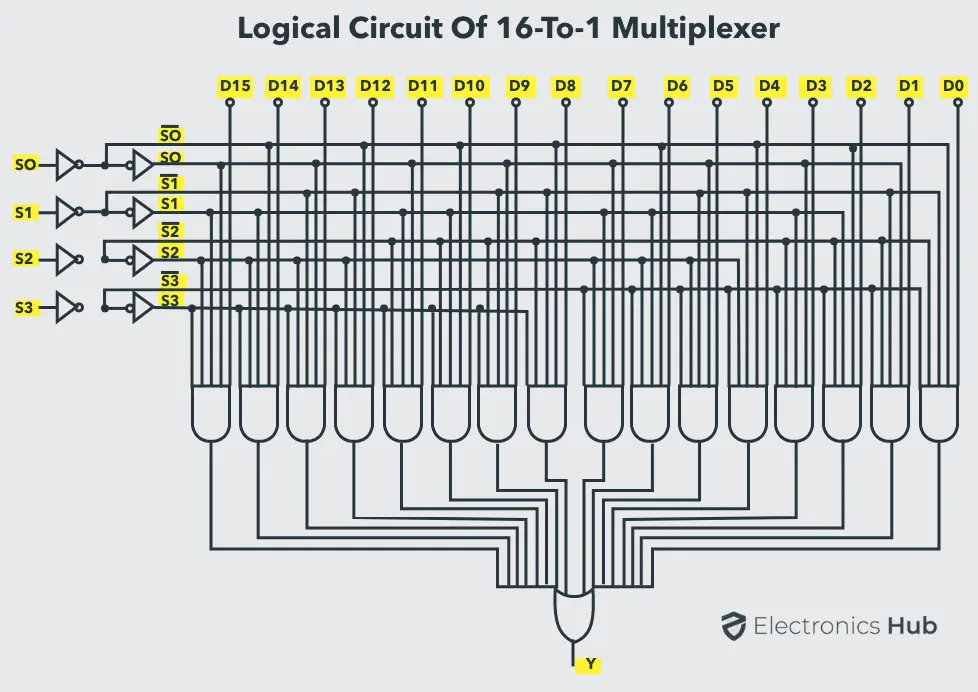
类似于 8 到 1 多路复用器，我们可以使用低阶多路复用器（如 8 到 1、4 到 1 和 2 到 1）来实现 16 到 1 多路复用器。下图展示了使用两个 8 到 1 多路复用器和一个 2 到 1 多路复用器实现的 16 到 1 多路复用器的框图。

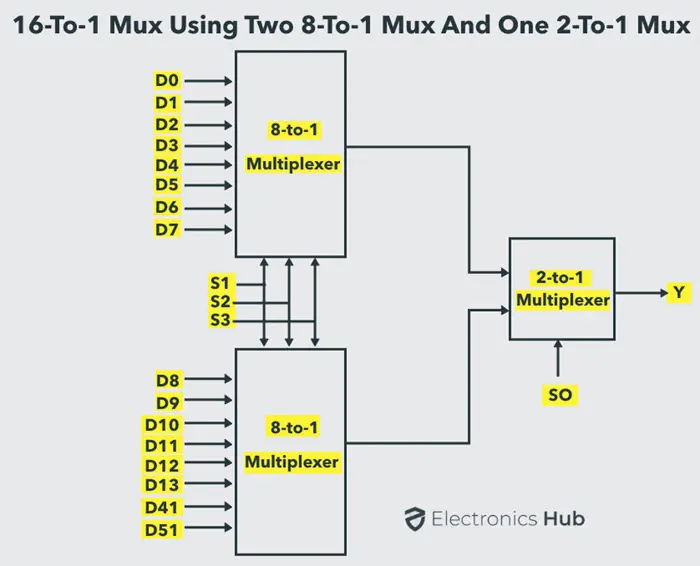
进一步地，我们可以在上述图中使用两个 4 到 1 多路复用器和一个 2 到 1 多路复用器来实现每个 8 到 1 多路复用器。

多路复用器的应用

在各种数字系统应用中，多路复用器的使用非常广泛。由于它们允许多个输入独立连接到单一输出，因此多路复用器在多种应用中都有使用，包括数据路由、逻辑函数发生器、控制序列器、并行到串行转换器等。

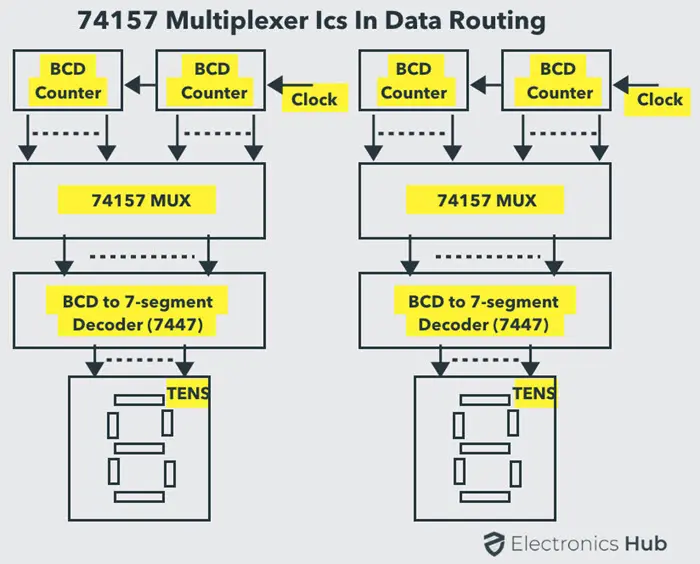
• 数据路由：多路复用器广泛用于数据路由应用，将数据从多个源路由到一个特定的目的地。一个应用示例包括依次显示两个多位 BCD 计数器的内容。在这种应用中，使用 74157 多路复用器 IC 通过一组译码器和 LED 显示器选择并显示两个 BCD 计数器中的一个的内容。

• 逻辑函数发生器：多路复用器可以代替逻辑门生成逻辑表达式。它可以连接成复制任何真值表的逻辑。在这种情况下，它可以生成一组输入变量的布尔代数函数。由于多路复用器是一个单一的集成电路，这显著减少了执行逻辑函数所需的逻辑门或集成电路的数量。在这种应用中，多路复用器被视为逻辑函数发生器。

  例如，考虑以下逻辑图，使用 74151A 8 到 1 多路复用器实现三个输入的异或函数。这个多路复用器的工作方式与实现相同功能的逻辑门组合完全相同。输出 $F$ 在数据输入 $D_1$、$D_2$、$D_5$ 和 $D_6$ 时为 1，这些输入分别通过将选择线设置为 001、010、100 和 111 来选择。

• 并行到串行转换：多路复用器电路可以用于将并行数据转换为串行数据，以减少并行总线的数量，将它们转换为串行信号。这种转换在电信、测试与测量、军事/航空、数据通信应用中是必需的。

  在数字系统中，数据通常以并行方式处理以实现更高的速度。但是，为了在长距离上传输数据信号，我们需要更多的线路。在这种情况下，使用多路复用器将并行数据转换为串行形式。

  下图展示了使用 8 输入多路复用器进行并行到串行数据转换。来自数据输入或其他寄存器的并行数据被应用到多路复用器的 8 个输入线。

  多路复用器的选择码由一个 3 位计数器生成。每当计数器接收到一个时钟脉冲时，数据就会从多路复用器中以串行方式输出。

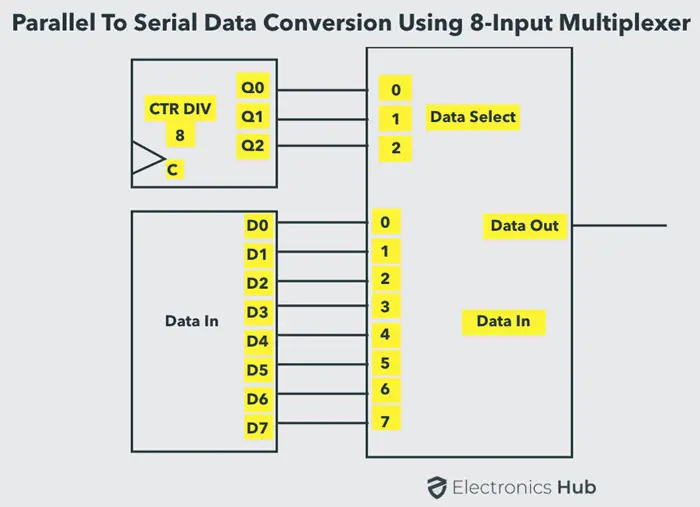
多路复用器的其他应用包括控制序列器、脉冲列发生器、编码器、寄存器到寄存器的数据传输、波形发生器等。

总结

本教程全面介绍了多路复用器（MUX）和多路复用技术。您学习了多路复用的基础知识、多路复用器、常用的多路复用器类型（如 2:1 MUX、4:1 MUX、8:1 MUX 和 16:1 MUX）、它们的布尔表达式、逻辑电路以及多路复用器的一些重要应用。

常见问题解答：多路复用器和多路复用

• 多路复用器与解复用器有何不同？ 多路复用器（MUX）将多个输入信号组合成一个输出信号，而解复用器（DEMUX）则将单个输入信号路由到多个输出中的一个。

• 选择多路复用器时需要考虑哪些关键因素？ 关键因素包括输入通道的数量、信号类型（模拟或数字）、速度要求、功耗以及与系统的兼容性。

• 多路复用器如何提高数据传输的效率？ 多路复用器允许多个信号通过单一信道传输，减少了对多条通信线路的需求，提高了带宽效率。

• 多路复用器如何影响信号完整性？ 多路复用器可能会由于串扰、噪声和传播延迟等因素导致信号退化。通过合理设计和屏蔽可以减轻这些影响。

• 是否存在基于软件的多路复用器？ 是的，基于软件的多路复用器确实存在，它们用于操作系统和网络软件等应用中，用于管理多条数据流和虚拟通道。