1.3 超前进位加法器

在并行加法器中，两个数的二进制加法只有在被加数和加数的所有位同时可用时才能开始计算。在并行加法器电路中，每个全加器阶段的进位输出连接到下一个更高阶阶段的进位输入，因此它也被称为逐位进位型加法器（ripple carry type adder）。

在这样的加法器电路中，只有当输入进位出现时，才可能产生任何阶段的和与进位输出。因此，在加法过程中会有一个相当大的时间延迟，这种延迟被称为进位传播延迟（carry propagation delay）。在任何组合电路中，信号必须通过门电路传播，然后才能在输出端获得正确的输出和。

考虑上图，其中和 $S_4$ 由相应的全加器在其输入信号被应用后立即产生。但进位输入 $C_4$ 直到进位 $c_3$ 达到其稳态值之前，都不会处于其最终稳态值。同样，$C_3$ 依赖于 $C_2$，而 $C_2$ 依赖于 $C_1$。因此，进位必须传播到所有阶段，以便输出 $S_4$ 和进位 $C_5$ 达到其最终稳态值。

传播时间等于典型门的传播延迟乘以电路中的门级数。例如，如果每个全加器阶段的传播延迟为 20 纳秒，那么 $S_4$ 将在 80 纳秒（20 × 4）后达到其最终正确值。如果我们增加阶段数以添加更多位数，这种情况会变得更糟。

因此，并行加法器中添加的位数的速度取决于进位传播时间。然而，信号必须在足够的时间内通过门电路传播，以产生正确或期望的输出。

以下是提高并行加法器速度以实现二进制加法的方法：

1. 使用更快的门电路：通过减少延迟来降低传播延迟。但每个物理逻辑门都有能力限制。
2. 增加电路复杂性：以减少进位延迟时间。有几种方法可以加快并行加法器的速度，其中一种常用的方法是采用前瞻进位加法（look-ahead carry addition），通过消除阶段间进位逻辑来实现。

前瞻进位加法器（Carry-Lookahead Adder）

前瞻进位加法器是一种快速并行加法器，它通过更复杂的硬件减少了传播延迟，因此成本更高。在这种设计中，加法器固定位组的进位逻辑被简化为两级逻辑，这实际上是逐位进位设计的转换。

这种方法利用逻辑门来查看被加数和加数的低阶位，以判断是否需要生成高阶进位。让我们详细讨论一下。

考虑上述全加器电路及其对应的真值表。如果我们定义两个变量：进位生成 $G_i$ 和进位传播 $P_i$，则有：

$P_i = A_i \oplus B_i$ $G_i = A_i \cdot B_i$

和输出和进位输出可以表示为：

$S_i = P_i \oplus C_i$ $C_{i+1} = G_i + P_i \cdot C_i$

其中，$G_i$ 是进位生成，当 $A_i$ 和 $B_i$ 均为1时，无论输入进位如何，都会产生进位。$P_i$ 是进位传播，它与从 $C_i$ 到 $C_{i+1}$ 的进位传播相关。

在4阶段前瞻进位加法器中，每个阶段的进位输出布尔函数可以表示为：

$C_1 = G_0 + P_0 \cdot C_{\text{in}}$ $C_2 = G_1 + P_1 \cdot C_1 = G_1 + P_1 \cdot G_0 + P_1 \cdot P_0 \cdot C_{\text{in}}$ $C_3 = G_2 + P_2 \cdot C_2 = G_2 + P_2 \cdot G_1 + P_2 \cdot P_1 \cdot G_0 + P_2 \cdot P_1 \cdot P_0 \cdot C_{\text{in}}$ $C_4 = G_3 + P_3 \cdot C_3 = G_3 + P_3 \cdot G_2 + P_3 \cdot P_2 \cdot G_1 + P_3 \cdot P_2 \cdot P_1 \cdot G_0 + P_3 \cdot P_2 \cdot P_1 \cdot P_0 \cdot C_{\text{in}}$

从上述布尔方程可以看出，$C_4$ 不必等待 $C_3$ 和 $C_2$ 传播，实际上 $C_4$ 与 $C_3$ 和 $C_2$ 同时传播。由于每个进位输出的布尔表达式是乘积之和，因此可以用一级与门后跟一个或门来实现。

下图展示了用于实现每个进位输出（$C_2$、$C_3$ 和 $C_4$）的三个布尔函数的逻辑图。

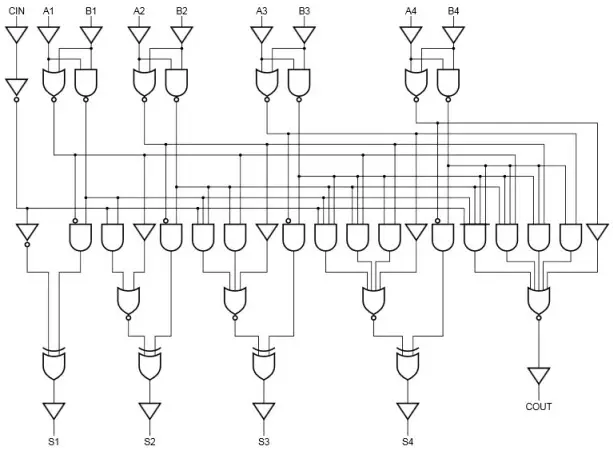
因此，可以使用前瞻进位方案实现4位并行加法器，以加快二进制加法的速度，如下图所示。在该电路中，每个和输出需要两个异或门。第一个异或门生成 $P_i$ 变量输出，而与门生成 $G_i$ 变量。

因此，在两级门电路中生成所有这些 $P$ 和 $G$ 信号。前瞻进位生成器允许所有这些 $P$ 和 $G$ 信号在其达到稳态值后传播，并在两级门电路的延迟后产生输出进位。因此，和输出 $S_2$ 到 $S_4$ 具有相等的传播延迟时间。

还可以通过级联多个4位加法器和进位逻辑来构建16位和32位并行加法器。16位前瞻进位加法器通过级联四个4位加法器并增加两级门延迟来构建，而32位前瞻进位加法器则通过级联两个16位加法器来形成。

在16位前瞻进位加法器中，获得 $C_{16}$ 和 $S_{15}$ 分别需要5级和8级门延迟，这比级联四个4位前瞻进位加法器块中 $C_{16}$ 和 $S_{15}$ 的9级和10级门延迟要少。同样，在32位加法器中，$C_{32}$ 和 $S_{31}$ 分别需要7级和10级门延迟，这比使用八个4位加法器实现32位加法器时的18级和17级门延迟要少。

前瞻进位加法器集成电路（ICs）

高速前瞻进位加法器由多个制造商以不同的位配置集成在集成电路中。还有许多单独的进位生成器集成电路可供选择，因此我们需要将它们与逻辑门连接起来以执行加法运算。

一个典型的前瞻进位生成器集成电路是 74182，它接受四对低电平有效的进位传播信号（$P_0, P_1, P_2, P_3$）和进位生成信号（$G_0, G_1, G_2, G_3$）以及一个高电平输入（$C_n$）。

它为四个二进制加法器组提供高电平进位（$C_{n+x}, C_{n+y}, C_{n+z}$）。该集成电路还通过低电平有效的进位传播和进位生成输出，为其他级别的前瞻提供便利。

74182集成电路提供的逻辑表达式如下：

另一方面，还有许多高速加法器集成电路将一组全加器与前瞻进位电路结合起来。这种集成电路最受欢迎的形式是 74LS83/74S283，它是一个4位并行加法器高速集成电路，包含四个相互连接的全加器和前瞻进位电路。

这种集成电路的功能符号如下图所示。它接收两个4位数 $A_3A_2A_1A_0$ 和 $B_3B_2B_1B_0$，并将输入进位 $C_{\text{in}0}$ 输入到最低有效位（LSB）位置。该集成电路产生输出和位 $S_3S_2S_1S_0$，以及进入最高有效位（MSB）位置的进位输出 $C_{\text{out}3}$。

通过级联两个或多个并行加法器集成电路，我们可以执行更大二进制数的加法，例如8位、24位和32位加法。