1.5 卡诺图或K-Map

卡诺图是由电信工程师莫里斯·卡诺（Maurice Karnaugh）于1953年在贝尔实验室提出的一种改进技术，源自“爱德华·维特希（Edward Veitch）的维特希图表”，它是一种用于简化或降低布尔表达式复杂性的方法。

卡诺图方法（K-map method）是布尔方程的图形化表示，通过布尔操作来降低求解它们的复杂性。这些可以被视为“真值表”的一种特殊或扩展版本。

什么是卡诺图？

卡诺图可以被解释为“一个包含 $2^k$ 个单元格的网格状数组，其中 $k$ 是要简化或优化的布尔表达式中的变量数量”。正如从真值表方法中评估的那样，卡诺图中的每个单元格将代表真值表的一行，每个单元格由一个正方形表示。

卡诺图中的单元格被安排得使得相邻行中的组合仅在一个变量上有所不同。卡诺图方法支持消除潜在的竞争条件，并允许快速识别。

通过使用卡诺图技术，我们可以简化包含任意数量变量的布尔表达式，例如2变量布尔表达式、3变量布尔表达式、4变量布尔表达式，甚至是复杂的7变量布尔表达式，这些表达式使用常规布尔定理和定律难以求解。

使用卡诺图进行最小化及其优势

卡诺图用于将布尔方程的真值表转换为最小化的与或表达式（SOP）形式。

• 简单易懂的基本规则：用于简化布尔表达式。
• 高效性：卡诺图方法比其他布尔代数简化技术更快、更高效。
• 直观性：卡诺图中的每一行都用正方形单元格表示，每个正方形代表一个最小项。
• 易于转换：将真值表转换为卡诺图，以及将卡诺图转换为与或表达式形式的方程非常方便。

将布尔方程转换为卡诺图有两种形式：

• 未优化形式：将1的数量转换为与或表达式方程中相同数量的乘积项（最小项）。
• 优化形式：减少与或表达式方程中的最小项数量。

卡诺图变量分组规则

在对卡诺图中的变量进行分组时，需要遵循以下规则：

1. 包含‘1’的单元格至少被使用一次：在简化过程中，包含‘1’的单元格必须至少被包含一次。
2. 可以多次使用包含‘1’的单元格：只要可能，包含‘1’的单元格可以被多次用于分组。
3. 分组中不应包含任何‘0’：分组中不能包含值为‘0’的单元格。
4. 分组应尽可能大：分组的大小应尽可能大，以简化布尔表达式。
5. 分组方向：分组可以是水平的或垂直的，但不允许对角线方向分组。

• 如果包含‘1’的单元格无法被分组，则应将其添加到最终表达式中。
• 分组可以重叠。
• 一个分组中的单元格数量必须是2的幂，例如1、2、4、8等。
• 分组可以环绕。由于卡诺图被视为球形或折叠的，角落的单元格（位于行或列的末端）应被视为相邻单元格。
• 卡诺图变量的分组方式有多种，因此得到的简化方程并不总是唯一的。
• 为了绘制卡诺图，布尔方程必须处于标准形式。

2变量卡诺图

2变量卡诺图包含4个单元格（$2^2$）。其外观如下图所示。

2变量（A和B）的可能最小项为 $A \cdot B$、$A \cdot \overline{B}$、$\overline{A} \cdot B$ 和 $\overline{A} \cdot \overline{B}$。变量的组合（A，B）和（A，$\overline{B}$）在顶部行的单元格中表示，而（$\overline{A}$，B）和（$\overline{A}$，$\overline{B}$）在底部行的单元格中表示。下表显示了2变量布尔函数的所有可能输出在卡诺图上的位置。

2变量卡诺图的一般表示如下图所示。

当使用卡诺图简化布尔方程时，我们将卡诺图中包含与项的每个单元格用1表示。之后，我们将可能的大小为2或4的相邻单元格分组。在更大的卡诺图中，我们可以将变量分组为更大的大小，如8或16。

变量的分组应呈矩形，这意味着分组必须通过垂直或水平组合相邻单元格来形成。不允许对角线形状或L形的分组。以下示例展示了2变量布尔方程的卡诺图简化。

示例

使用卡诺图简化给定的2变量布尔方程。

$F = X \cdot \overline{Y} + \overline{X} \cdot Y + \overline{X} \cdot \overline{Y}$

首先，我们为给定的方程构建真值表。

我们在方程中给出的输出项处放置1。

在这个卡诺图中，我们可以按照分组规则创建2个分组，一个是由（$\overline{X}$，Y）和（$\overline{X}$，$\overline{Y}$）项组合而成，另一个是由（X，$\overline{Y}$）和（$\overline{X}$，$\overline{Y}$）项组合而成。这里右下角的单元格在两个分组中都被使用了。 分组变量后，下一步是确定最小化表达式。

通过简化每个分组，我们得到最小化表达式的与项，例如通过从两个分组中提取公共项，即 $\overline{X}$ 和 $\overline{Y}$。因此，简化后的方程为 $\overline{X} + \overline{Y}$。

3变量卡诺图

对于一个3变量布尔函数，有8种可能的输出最小项。使用3变量表示所有最小项的一般表示如下。

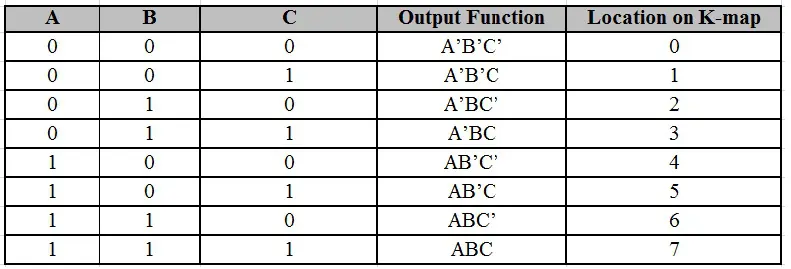
典型的3变量卡诺图如下图所示。可以看出，列10和11的位置被交换，以便在相邻单元格之间只改变一个变量。这种修改将有助于最小化逻辑。

在3变量卡诺图中，最多可以分组8个单元格，其他可能性为1、2和4。

示例

使用卡诺图简化给定的3变量布尔方程。

$F = \overline{X} \cdot Y \cdot Z + \overline{X} \cdot \overline{Y} \cdot Z + X \cdot Y \cdot \overline{Z} + \overline{X} \cdot \overline{Y} \cdot \overline{Z} + X \cdot Y \cdot Z + X \cdot \overline{Y} \cdot \overline{Z}$

首先，我们为给定的方程构建真值表。

我们在方程中给出的输出项处放置1。

3变量卡诺图有8个单元格（$2^3$）。其外观如下图所示。

最大的分组大小为8，但根据可能性，我们也可以形成大小为4和2的分组。在3变量卡诺图中，我们将卡诺图的最左列视为最右列的相邻列。因此，大小为4的分组如下图所示。

在两个项中，我们都有‘Y’作为公共项。因此，大小为4的分组简化为与项 Y。为了包含每个值为1的单元格，我们将剩余的单元格分组以形成大小为2的分组，如下图所示。

大小为2的分组没有公共变量，因此它们用其变量及其共轭表示。因此，简化后的方程为 $X \cdot \overline{Z} + Y + \overline{X} \cdot Z$。在这个方程中，无法进一步简化。

4变量卡诺图

在4变量布尔函数中，有16种可能的最小项。使用4变量表示最小项的一般表示如下。

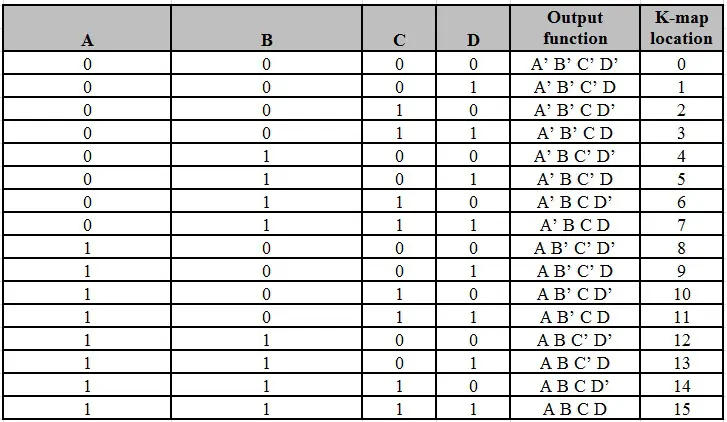
典型的4变量卡诺图如下图所示。可以看出，10和11的列和行都被交换了。

可以分组的单元格数量为1、2、4、8和16。

示例

使用卡诺图简化给定的4变量布尔方程。 $F(W, X, Y, Z) = \sum(1, 5, 12, 13)$

解：$F(W, X, Y, Z) = \sum(1, 5, 12, 13)$

通过准备卡诺图，我们可以将给定的布尔方程简化为

$F = W \cdot \overline{Y} \cdot Z + \overline{W} \cdot \overline{Y} \cdot Z$

5变量卡诺图

一个5变量布尔函数最多可以有32个最小项。所有可能的最小项如下表示。

A	B	C	D	E	OUTPUT FUNCTIONS	LOCATION ON K-MAP
0	0	0	0	0	$\overline{A}\overline{B}\overline{C}\overline{D}\overline{E}$	0
0	0	0	0	1	$\overline{A}\overline{B}\overline{C}\overline{D}E$	1
0	0	0	1	0	$\overline{A}\overline{B}\overline{C}D\overline{E}$	2
0	0	0	1	1	$\overline{A}\overline{B}\overline{C}DE$	3
0	0	1	0	0	$\overline{A}\overline{B}C\overline{D}\overline{E}$	4
0	0	1	0	1	$\overline{A}\overline{B}C\overline{D}E$	5
0	0	1	1	0	$\overline{A}\overline{B}CD\overline{E}$	6
0	0	1	1	1	$\overline{A}\overline{B}CDE$	7
0	1	0	0	0	$\overline{A}B\overline{C}\overline{D}\overline{E}$	8
0	1	0	0	1	$\overline{A}B\overline{C}\overline{D}E$	9
0	1	0	1	0	$\overline{A}B\overline{C}D\overline{E}$	10
0	1	0	1	1	$\overline{A}B\overline{C}DE$	11
0	1	1	0	0	$\overline{A}BC\overline{D}\overline{E}$	12
0	1	1	0	1	$\overline{A}BC\overline{D}E$	13
0	1	1	1	0	$\overline{A}BCD\overline{E}$	14
0	1	1	1	1	$\overline{A}BCDE$	15
1	0	0	0	0	$A\overline{B}\overline{C}\overline{D}\overline{E}$	16
1	0	0	0	1	$A\overline{B}\overline{C}\overline{D}E$	17
1	0	0	1	0	$A\overline{B}\overline{C}D\overline{E}$	18
1	0	0	1	1	$A\overline{B}\overline{C}DE$	19
1	0	1	0	0	$A\overline{B}C\overline{D}\overline{E}$	20
1	0	1	0	1	$A\overline{B}C\overline{D}E$	21
1	0	1	1	0	$A\overline{B}CD\overline{E}$	22
1	0	1	1	1	$A\overline{B}CDE$	23
1	1	0	0	0	$AB\overline{C}\overline{D}\overline{E}$	24
1	1	0	0	1	$AB\overline{C}\overline{D}E$	25
1	1	0	1	0	$AB\overline{C}D\overline{E}$	26
1	1	0	1	1	$AB\overline{C}DE$	27
1	1	1	0	0	$ABC\overline{D}\overline{E}$	28
1	1	1	0	1	$ABC\overline{D}E$	29
1	1	1	1	0	$ABCD\overline{E}$	30
1	1	1	1	1	$ABCDE$	31

5变量卡诺图

在5变量卡诺图中，我们有32个单元格，如下所示。它由 $F(A, B, C, D, E)$ 表示。它被分为两个16个单元格的网格，其中一个变量（A）在一个网格中为0，在另一个网格中为1。

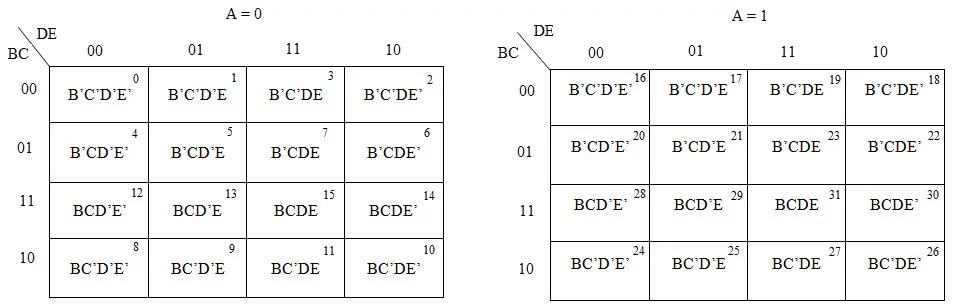
示例

使用卡诺图简化给定的5变量布尔方程。

$f(A, B, C, D, E) = \sum m(0, 5, 6, 8, 9, 10, 11, 16, 20, 21, 25, 26, 27)$

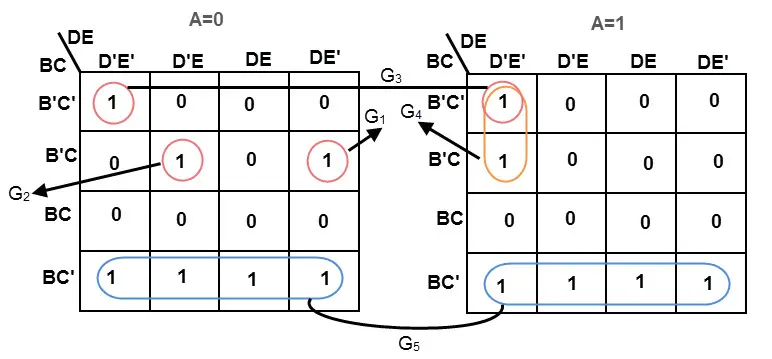
带“不关心”条件的卡诺图

“不关心”条件用于替换空单元格，以形成可能的变量分组。它们可以根据分组中的相邻变量被用作0或1。“不关心”条件的单元格用星号（*）符号表示，与正常的0和1一起。

在变量分组中，我们也可以忽略“不关心”条件。“不关心”条件在分组大量变量时非常有用。

带“不关心”条件的表达式最小化

我们可以通过为“不关心”条件分配0或1来找到它们的相对函数，从而最小化布尔表达式。如果布尔方程中有 $n$ 个“不关心”条件，则获得的函数数量将是 $2^n$。

使用卡诺图实现BCD到格雷码的转换器

格雷码是一种数字序列，其中两个连续的数字只有一位不同。这种编码以其发明者“弗兰克·格雷”（Frank Gray）的名字命名。他在1953年获得了使用格雷码的专利。

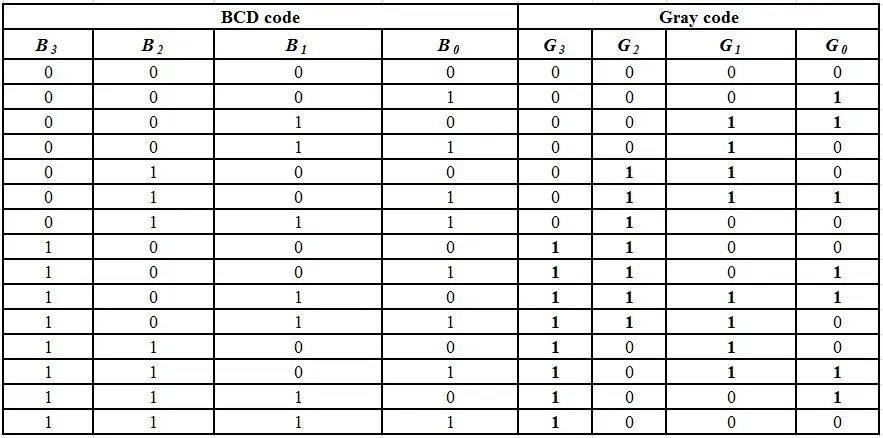
我们可以通过卡诺图简化来将二进制编码的十进制（BCD）码转换为格雷码。

BCD码和格雷码的对照表

$G_3$ 的卡诺图

$G_2$ 的卡诺图

$\text{G2的方程} = \overline{B_3} B_2 + B_3 \overline{B_2} = B_3 \oplus B_2$

$G_1$ 的卡诺图

$\text{G1的方程} = \overline{B_1} B_2 + B_1 \overline{B_2} = B_1 \oplus B_2$

$G_0$ 的卡诺图

$\text{G0的方程} = \overline{B_1} B_0 + B_1 \overline{B_0} = B_1 \oplus B_0$

使用逻辑门实现BCD到格雷码转换的电路如下所示。使用了两个异或门（Ex-OR）和一个或门。