1.3 布尔函数或开关函数

布尔逻辑在与或表达式（Sum of Products，SOP）和或与表达式（Product of Sums，POS）形式中是数字电路设计的基础，提供了一种系统化的方法来表达和简化逻辑表达式。SOP形式通过将多个与（AND）操作的项进行或（OR）操作组合，而POS形式则通过将多个或（OR）操作的项进行与（AND）操作组合，两者都能高效地表示复杂的逻辑电路。这些形式在优化数字系统以实现硬件效率和计算速度方面起着关键作用，是理解和实现各种应用中数字逻辑的基石。

布尔表达式的逻辑表示

使用开关器件（如晶体管）会引出布尔代数的一个特殊情况，称为开关代数。在开关代数中，所有变量仅取两个值，即0和1。

在布尔代数中，0用于表示逻辑门的“断开”状态或“假”状态，而1用于表示逻辑门的“闭合”状态或“真”状态。布尔表达式是由变量、常量（0表示假，1表示真）以及逻辑运算符组成的表达式，其结果为真或假。布尔函数是布尔表达式的代数形式，一个含 $n$ 个变量的布尔函数表示为 $f(x_1, x_2, x_3, \dots, x_n)$。通过使用布尔定律和定理，我们可以简化数字电路的布尔函数。布尔函数的不同表示方法如下：

• 与或表达式（SOP）形式
• 或与表达式（POS）形式
• 标准形式

标准形式有两种：

• 最小项之和（或称为标准SOP）
• 最大项之积（或称为标准POS）

布尔函数可以用与非门（NAND gates）表示，也可以通过卡诺图（Karnaugh map，K-map）方法进行简化。通过使用这两种标准形式，我们可以使布尔表达式更加标准化，从而使得实现、演化和简化过程更加容易和系统化。

与或表达式（SOP）形式

与或表达式（SOP）形式是一种简化逻辑门布尔表达式的方法（或形式）。在这种布尔函数的SOP表示形式中，变量通过与（AND）操作形成乘积项，然后将所有这些乘积项通过或（OR）操作组合起来以获得最终函数。

与或表达式形式可以通过使用布尔加法操作将两个或多个乘积项相加（或求和）来形成。这里，乘积项通过与（AND）操作定义，而和项通过或（OR）操作定义。

与或表达式形式也被称为析取范式（Disjunctive Normal Form），因为乘积项通过或（OR）操作组合，析取操作是逻辑或。与或表达式形式也被称为标准SOP形式。

SOP形式表示最适合用于现场可编程门阵列（Field Programmable Gate Arrays，FPGA）。

SOP形式示例

• $AB + ABC + CDE$
• $\overline{(AB)} + ABC + CD\overline{E}$

可以通过以下步骤获得SOP形式：

1. 为每个产生高电平输出的输入组合写出一个与（AND）项。
2. 如果变量的值为1，则写出输入变量；如果变量的值为0，则写出该变量的补码。
3. 将与（AND）项通过或（OR）操作组合以获得输出函数。

例如：多数函数的布尔表达式 $F = \overline{A}BC + A\overline{B}C + AB\overline{C} + ABC$

SOP形式真值表：

现在写出产生高电平输出的输入变量组合。 $F = AB + BC + AC$.

验证：

根据幂等律，我们知道

$[(ABC + ABC)] + ABC = (ABC + ABC) = ABC$

现在函数 $F = \overline{A}BC + A\overline{B}C + AB\overline{C} + ABC$

$= \overline{A}BC + A\overline{B}C+AB\overline{C} + ([ABC + ABC]+ABC)$ $= (ABC + AB\overline{C}) + (ABC + A\overline{B}C) + (ABC + \overline{A}BC)$ $= AB(C + \overline{C}) + A(B + \overline{B})C + (\overline{A} + A)BC$ $= AB + BC + AC$

或与表达式（POS）形式

或与表达式（POS）形式是一种简化逻辑门布尔表达式的方法（或形式）。在这种POS形式中，所有变量通过或（OR）操作组合，形成和项。

然后将所有这些和项通过与（AND）操作组合在一起以获得或与表达式形式。这种形式与SOP形式完全相反，因此也可以被称为“SOP形式的对偶形式”。

这里，和项通过或（OR）操作定义，而乘积项通过与（AND）操作定义。当两个或多个和项通过布尔或（OR）操作相乘时，得到的输出表达式将处于或与表达式形式或POS形式。

或与表达式形式也被称为合取范式（Conjunctive Normal Form），因为和项通过与（AND）操作组合，合取操作是逻辑与。或与表达式形式也被称为标准POS形式。

POS形式示例

• $(A+B) \times (A + B + C) \times (C +D)$
• $\overline{(A+B)} \times (C + D + \overline{E})$

可以通过以下步骤获得POS形式：

1. 为每个产生低电平输出的输入组合写出一个或（OR）项。
2. 如果变量的值为0，则写出输入变量；如果变量的值为1，则写出该变量的补码。
3. 将或（OR）项通过与（AND）操作组合以获得输出函数。

例如：多数函数的布尔表达式 $F = (A + B + C)(A + B + \overline{C})(A + \overline{B} + C)(\overline{A} + B + C)$

POS形式真值表：

现在写出产生高电平输出的输入变量组合。 $F = AB + BC + AC$.

验证：

根据幂等律，我们知道

$[(A + B + C)(A + B + C)](A + B + C) = [(A + B + C)](A + B + C) = (A + B + C)$

现在函数

$F = (A + B)(B + C)(A + C)$ $= (A + B + C)(A + B + \overline{C})(A + \overline{B} + C)(\overline{A} + B + C)$ $= [(A + B + C)(A + B + C)](A + B + C)(A + B + \overline{C})(A + \overline{B} + C)(\overline{A} + B + C)$ $= [(A + B + C)(A + B + \overline{C})][(A + B + C)(\overline{A} + B + C)][(A + B + C)(A + \overline{B} + C)]$ $= [(A + B) + (C \cdot \overline{C})][(B + C) + (A \cdot \overline{A})][(A + C) + (B \cdot \overline{B})]$ $= [(A + B) + 0][(B + C) + 0][(A + C) + 0] = (A + B)(B + C)(A + C)$

标准形式（标准SOP和POS形式）

任何以最小项之和或最大项之积的形式表示的布尔函数，都被称为其“标准形式”。

它主要涉及两个布尔项：“最小项”和“最大项”。

当布尔表达式的SOP形式处于标准形式时，其每个乘积项被称为“最小项”。因此，乘积和函数的标准形式也被称为“最小项标准形式”或“最小项之和”或“标准SOP形式”。

同样，当布尔表达式的POS形式处于标准形式时，其每个和项被称为“最大项”。因此，和的乘积函数的标准形式也被称为“最大项标准形式”或“和的乘积”或“标准POS形式”。

最小项

最小项被定义为 $n$ 个变量的乘积项，其中每个变量将以补码或非补码的形式出现一次。最小项用 $m_i$ 表示，其中 $i$ 的范围为 $0 \leq i < 2^n$。

如果变量的值为0，则变量处于补码形式；如果变量的值为1，则变量处于非补码形式。

对于一个包含两个变量（$x$ 和 $y$）的布尔函数，可能的最小项为：

$\overline{x}\overline{y}, \quad \overline{x}y, \quad x\overline{y}, \quad xy.$

对于一个包含三个变量（$x$、$y$ 和 $z$）的布尔函数，可能的最小项为：

$\overline{x}\overline{y}\overline{z}, \quad \overline{x}\overline{y}z, \quad \overline{x}y\overline{z}, \quad \overline{x}yz, \quad x\overline{y}\overline{z}, \quad x\overline{y}z, \quad xy\overline{z}, \quad xyz$

1-最小项是指函数 $F = 1$ 的最小项。 0-最小项是指函数 $F = 0$ 的最小项。 任何布尔函数都可以表示为其1-最小项的和（或）。方程的表示形式为

$F(\text{变量列表}) = \sum(\text{1-最小项索引列表})$

例如：$F(x, y, z) = \sum(3, 5, 6, 7)$

函数的反函数可以表示为其0-最小项的和（或）。方程的表示形式为

$F'(\text{变量列表}) = \sum(\text{0-最小项索引列表})$

例如：$F'(x, y, z) = \sum(0, 1, 2, 4)$

最小项的标准形式（最小项标准形式）的示例：

i $Z = XY + X\overline{Z}$

ii $F = XY\overline{Z} + \overline{X}YZ + \overline{X}Y\overline{Z} + X\overline{Y}Z + XYZ$

在标准SOP形式中，对于 $n$ 个变量，可能的乘积项的最大数量由 $2^n$ 给出。因此，对于包含两个变量的方程，乘积项为 $2^2 = 4$。同样，对于包含三个变量的方程，乘积项为 $2^3 = 8$。

最大项

最大项被定义为 $n$ 个变量的乘积，其中 $0 \leq i < 2^n$。最大项用 $M_i$ 表示。在最大项中，如果变量的值为1，则变量被补码；如果变量的值为0，则变量不被补码。

对于一个包含两个变量（$x$ 和 $y$）的布尔函数，可能的最大项为：

$x + y, \quad x + \overline{y}, \quad \overline{x} + y, \quad \overline{x} + \overline{y}.$

对于一个包含三个变量（$x$、$y$ 和 $z$）的布尔函数，可能的最大项为：

$x + y + z, \quad x + y + \overline{z}, \quad x + \overline{y} + z, \quad x + \overline{y} + \overline{z}, \quad \overline{x} + y + z, \quad \overline{x} + y + \overline{z}, \quad \overline{x} + \overline{y} + z, \quad \overline{x} + \overline{y} + \overline{z}$

1-最大项是指函数 $F = 1$ 的最大项。 0-最大项是指函数 $F = 0$ 的最大项。 任何布尔函数都可以表示为其0-最大项的乘积（与）。方程的表示形式为

$F(\text{变量列表}) = \prod(\text{0-最大项索引列表})$

例如：$F(x, y, z) = \prod(0, 1, 2, 4)$

函数的反函数可以表示为其1-最大项的乘积（与）。方程的表示形式为

$F'(\text{变量列表}) = \prod(\text{1-最大项索引列表})$

例如：$F'(x, y, z) = \prod(3, 5, 6, 7)$

最大项的标准形式（最大项标准形式）的示例：

i. $Z = (X + Y)(X + \overline{Y})$

ii. $F = (\overline{X} + Y + \overline{Z})(\overline{X} + Y + Z)(\overline{X} + \overline{Y} + \overline{Z})$

在标准POS形式中，对于 $n$ 个变量，可能的和项的最大数量由 $2^n$ 给出。因此，对于包含两个变量的方程，和项为 $2^2 = 4$。同样，对于包含三个变量的方程，和项为 $2^3 = 8$。

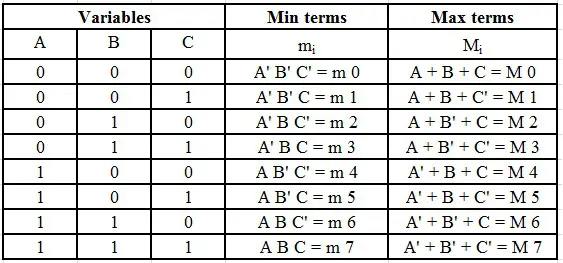
$2^n$ 最小项和 $2^n$ 最大项的表格

下表将帮助你理解3个变量的最小项和最大项的表示方法。

标准形式之间的转换

我们可以将一种标准形式的方程表示为另一种标准形式，即我们可以将SOP形式的方程表示为POS形式，反之亦然。为了转换标准方程，我们在列出方程中未包含的索引号后，交换 $\Sigma$ 和 $\Pi$ 符号。

关于布尔函数需要记住的重要一点是，SOP和POS形式彼此为对偶形式。转换方程的标准形式需要遵循以下两个步骤：

步骤1：在方程中交换操作符号 $\Sigma$ 和 $\Pi$。

步骤2：使用德摩根的对偶性原理对布尔函数的索引号进行操作，或者写出在给定方程形式中未出现的项的索引。

SOP形式转换为POS形式

要将SOP形式转换为POS形式，首先需要将 $\Sigma$ 改为 $\Pi$，然后写出给定布尔函数中缺失变量的数值索引。

示例：

SOP函数

$F = \sum_{A, B, C} (0, 2, 3, 5, 7) = \overline{A}\overline{B}\overline{C} + A\overline{B}\overline{C} + A\overline{B}C + AB\overline{C} + ABC$

转换为POS形式：

步骤1：将操作符号改为 $\Pi$。

步骤2：写出缺失的项的索引，即001、100和110。现在为这些记录的项写出和形式。

$001 = (A + B + C), \quad 100 = (A + \overline{B} + \overline{C}), \quad 110 = (A + \overline{B} + \overline{C})$

将新的方程以POS形式写出：

$F = \prod_{A, B, C} (1, 4, 6) = (A + B + C) \times (A + \overline{B} + \overline{C}) \times (A + \overline{B} + \overline{C})$

POS形式转换为SOP形式

要将POS形式转换为SOP形式，首先需要将 $\Pi$ 改为 $\Sigma$，然后写出给定布尔函数中缺失变量的数值索引。

示例：

POS函数

$F = \prod_{A, B, C} (2, 3, 5) = A\overline{B}C' + A\overline{B}C + ABC'$

转换为SOP形式：

步骤1：将操作符号改为 $\Sigma$。

步骤2：写出缺失的项的索引，即 000、001、100、110 和 111。现在为这些记录的项写出乘积形式。

$000=\overline{A} \cdot \overline{B} \cdot C$ $100=A \cdot \overline{B} \cdot \overline{C}$ $110=A \cdot B \cdot \overline{C}$ $111=A \cdot B \cdot C$

将新的方程以SOP形式写出：

$F = \sum_{A, B, C} (0, 1, 4, 6, 7) = (\overline{A} \cdot \overline{B} \cdot \overline{C}) + (\overline{A} \cdot \overline{B} \cdot C) + (A \cdot \overline{B} \cdot \overline{C}) + (A \cdot B \cdot \overline{C}) + (A \cdot B \cdot C)$

SOP形式转换为标准SOP形式（或最小项标准形式）

我们可以通过将SOP形式方程中的每个乘积项转换为包含所有变量的形式，从而将SOP形式方程转换为标准SOP形式。这可以通过使用布尔代数定律 $A + A' = 1$ 并按照以下步骤完成：

步骤1：

将每个非标准乘积项乘以其缺失变量及其补码的和，从而得到2个乘积项。

步骤2：

重复步骤1，直到所有得到的乘积项都包含所有变量。

通过这两个步骤，我们可以将SOP函数转换为标准SOP函数。在这个过程中，对于函数中每个缺失的变量，乘积项的数量将翻倍。

示例：

将非标准SOP函数 $F = xy + xz + yz$ 转换为标准SOP形式。

解：

$F= xy + xz + yz$ $= xy(z + \overline{z}) + x(y + \overline{y})z + (x + \overline{x})yz$ $= xyz + xy\overline{z} + x\overline{y}z + \overline{x}yz$

标准SOP形式为：

$F = xyz + xy\overline{z} + x\overline{y}z + \overline{x}yz$

POS形式转换为标准POS形式（或最大项标准形式）

我们可以通过将POS形式方程中的每个和项转换为包含所有变量的形式，从而将POS形式方程转换为标准POS形式。这可以通过使用布尔代数定律 $A \cdot \overline{A} = 0$ 并按照以下步骤完成：

步骤1：

将每个非标准和项加上其缺失变量及其补码的乘积，从而得到2个和项。

步骤2：

应用布尔代数定律 $A + BC = (A + B)(A + C)$。

步骤3：

重复步骤1，直到所有得到的和项都包含所有变量。

通过这三个步骤，我们可以将POS函数转换为标准POS函数。

示例：

$F = (\overline{A} + B + C) \times (\overline{B} + C + \overline{D}) \times (A + \overline{B} + \overline{C} + D)$

在第一个项中，变量 $D$ 或 $\overline{D}$ 缺失，因此我们加上 $D \cdot \overline{D} = 1$。于是，

$(\overline{A} + B + C + D \cdot \overline{D}) = (\overline{A} + B + C + D) \times (\overline{A} + B + C + \overline{D})$

同样，在第二个项中，变量 $A$ 或 $\overline{A}$ 缺失，因此我们加上 $A \cdot \overline{A} = 1$。于是，

$(\overline{B} + C + \overline{D} + A \cdot \overline{A}) = (A + \overline{B} + C + \overline{D}) \times (\overline{A} + \overline{B} + C + \overline{D})$

第三个项已经包含所有变量，因此已经是标准形式。现在函数的标准POS形式为：

$F = (\overline{A} + B + C + D) \times (\overline{A} + B + C + \overline{D}) \times (A + \overline{B} + C + \overline{D}) \times (\overline{A} + \overline{B} + C + \overline{D}) \times (A + \overline{B} + \overline{C} + D)$