1.6 八进制数系统

在前面的部分中，我们已经学习了十进制、二进制和十六进制数系统。这种数系统与十六进制系统非常相似。我们知道，十进制系统以10为基数，因为它使用0到9的数字；二进制系统的基数为2，因为它使用0和1这两个数字；十六进制数系统以16为基数，因此该系统使用16个数字，即从0到15。同样，“八进制数系统”仅使用8个数字来表示数字，因此得名为“八进制”（0-7）。

八进制数系统

在十六进制数系统中，我们将二进制数字表示为一组4位数字（$2^4 = 16$）。在八进制数系统中，我们将二进制数字表示为一组3位数字（$2^3 = 8$）。八进制数系统使用从0到7的8个数字，它们分别是0、1、2、3、4、5、6和7。

因此，八进制数的每一位都是由0到7的数字组成。与其他数系统相比，八进制数系统的主要优势在于，当我们在计算机上工作时，将数字写成八进制形式比写成二进制形式更容易。尤其是当我们处理大量的二进制数字时，建议将它们按每组3位进行分组，这样可以减少出错的机会。八进制数系统的另一个优点是，八进制与二进制之间的转换比其他转换更为简单。

这种数系统的基数为8。例如：$(501)_8$，$(480)_8$。

一个数字的权重会随着8的幂次增加而增加，如下所示：

让我们通过一个例子来理解八进制数如何表示为一组3位数字。

因此，二进制数100011010在八进制中表示为$(432)_8$。

八进制数的转换

八进制数可以转换为二进制、十进制数系统，也可以转换为十六进制数。以下是一些具体的转换方法。

从二进制转换为八进制数

要将二进制数转换为八进制数，首先需要将二进制字符串按每组3位进行划分。将每组对应的数字写出来，即可得到该二进制数的八进制表示。

例1：将110111100010转换为八进制。

将二进制数按每组3位划分：

$110\ 111\ 100\ 010$

对应的八进制数字为：

$6\ 7\ 4\ 2$

因此，$(110111100010)_2 = (6742)_8$。

从八进制数转换为二进制数
将八进制数转换为二进制数的过程是二进制转换为八进制的逆过程。即八进制数的每一位都应写成其对应的二进制形式，将所有二进制数字组合起来，即可得到所需的二进制数。

例1：将$(43628)_8$转换为二进制。

将每一位对应的二进制数写出来：

$\begin{aligned} 4 &\rightarrow 100 \\ 3 &\rightarrow 011 \\ 6 &\rightarrow 110 \\ 2 &\rightarrow 010 \\ 8 &\rightarrow 100 \\ \end{aligned}$

因此，$(43628)_8 = (100011110010100)_2$。

从十进制转换为八进制数
通过反复除以8的方法可以将十进制数转换为八进制数。在每个阶段的余数将给出所需的八进制数。

请参见以下示例。

例1：将$(159)_{10}$转换为八进制。

$\begin{aligned} 159 \div 8 &\rightarrow \text{商 } 19, \text{ 余数 } 7 \text{（最低有效位）} \\ 19 \div 8 &\rightarrow \text{商 } 2, \text{ 余数 } 3 \\ 2 \div 8 &\rightarrow \text{商 } 0, \text{ 余数 } 2 \text{（最高有效位）} \\ \end{aligned}$

因此，$(159)_{10} = (237)_8$。

例2：将$(80)_{10}$转换为八进制。

$\begin{aligned} 80 \div 8 &\rightarrow \text{商 } 9, \text{ 余数 } 8 \text{（最低有效位）} \\ 9 \div 8 &\rightarrow \text{商 } 1, \text{ 余数 } 1 \\ 1 \div 8 &\rightarrow \text{商 } 0, \text{ 余数 } 1 \text{（最高有效位）} \\ \end{aligned}$

因此，$(80)_{10} = (118)_8$。

从八进制数转换为十进制数
通过将每一位数字乘以其位置值，可以将八进制数转换为十进制数。也就是说，每一位数字都乘以8的幂次，根据其位置进行计算。

让我们来看一个例子。

例1：将$(51)_8$转换为十进制。

$\begin{aligned} &\text{位置权重} &8^1 &8^0 \\ &\text{位置值} &8 &1 \\ &\text{八进制数字} &5 &1 \\ &\text{等效十进制数} &= 5 \times 8^1 + 1 \times 8^0 \\ &= 40 + 1 \\ &= 41 \end{aligned}$

因此，$(51)_8 = (41)_{10}$。

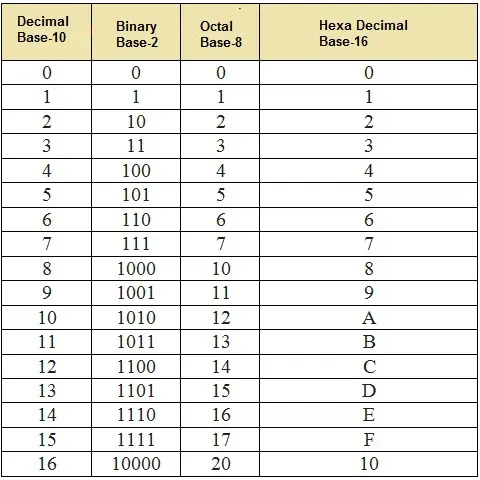
同样，也可以将八进制数转换为其他数系统。下表显示了与其他数系统的等效值。

八进制数的表示

八进制数以基数8表示，因为它们仅使用8个数字，如上所述。八进制数中每一位的权重如下所示。

八进制数的表示方式与其他数系统类似。在以下八进制数系统中：

$\begin{aligned} 10 &\text{ 不是十，而是 } (1 \times 8) + (0 \times 8) \\ 20 &\text{ 不是二十，而是 } (2 \times 8) + (0 \times 8) \\ \end{aligned}$

总结

我们将3位二进制数字表示为1位八进制数字，如上所示。同样，最高的两位八进制数$(77)_8$可以表示63位二进制数字。类似地，最高的三位八进制数$(777)_8$可以表示511位二进制数字。最高的四位八进制数$(7777)_8$可以表示4095位二进制数字。

八进制数系统使用从0到7的8个数字（0、1、2、3、4、5、6和7）。在八进制数系统中，一个数字的权重会随着8的幂次增加而增加。十进制数可以通过反复除以8的方法转换为八进制数。