1.3 惠斯通电桥
在本教程中,我们将学习惠斯通电桥(Wheatstone Bridge)。我们将探讨惠斯通电桥的工作原理、一些示例电路以及一些重要的应用。
电阻测量及其类型
在模拟电子学的世界中,我们会遇到各种信号,其中一些通过�电阻的变化来测量,而另一些则通过电感和电容的变化来测量。
如果我们考虑电阻,大多数工业传感器(如温度、应变、湿度、位移、液位等)都会因相应物理量的变化而产生电阻值的变化。因此,对于每一个基于电阻的传感器,都需要进行信号调理。
例如,我们可以想到的最简单设备是光敏电阻(LDR)。顾名思义,光敏电阻是一种电阻值会根据落在其上的光量而变化的设备。
一般来说,电阻测量分为三种类型:
- 低电阻测量
- 中等电阻测量
- 高电阻测量
如果电阻测量的范围是从几微欧姆到几毫欧姆,那么它被认为是低电阻测量。这种测量主要用于研究目的。如果测量范围是从 1 欧姆到几百千欧姆,通常被称为中等电阻测量。普通电阻、电位器、热敏电阻等的测量属于这一类别。
非常高电阻的测量范围是从几兆欧姆到大于 100 兆欧姆。为了找到中等值的电阻,使用了不同的方法,但大多数情况下使用的是惠斯通电桥。
什么是惠斯通电桥?
电桥网络或电路是最受欢迎且常用的电气工具之一,常用于测量电路、传感器电路、开关电路以及振荡器中。
惠斯通电桥是最常见且最简单的电桥网络/电路之一,它可以非常精确地用于测量电阻。然而,惠斯通电桥通常与传感器一起用于测量物理量,如温度、压力、应变等。
在需要测量传感器中微小电阻变化的应用中,会使用惠斯通电桥。它用于将传感器电阻的变化转换为电压的变化。这种电桥与运算放大器的组合在工业中被广泛用于各种传感器和传感器。
例如,当热敏电阻受到温度变化时,其电阻会发生变化。同样,应变片在受到压力、力或位移时,其电阻也会发生变化。根据应用类型,惠斯通电桥可以在平衡状态或不平衡状态下工作。
惠斯通电桥由四个电阻(、、 和 )组成,它们以菱形的方式连接,直流电源连接在菱形的顶部和底部点(电路中的 C 和 D 点),输出则从另外两个端点(电路中的 A 和 B 点)取出。
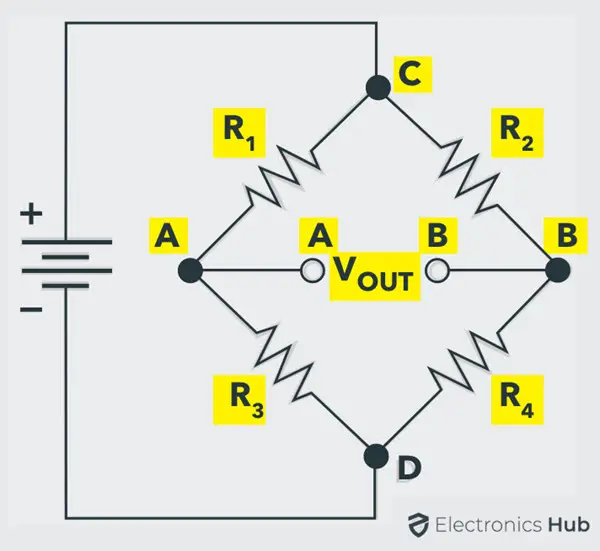
这种电桥通过将其与已知电阻值进行比较,可以非常精确地找到未知电阻。在这种电桥中,使用零点或平衡条件来找到未知电阻。
为了使电桥处于平衡状态,A 和 B 点的输出电压必须等于 0。从上述电路来看:
如果电桥处于平衡状态,则有:
为了简化上述电路的分析,让我们将其重新绘制如下:
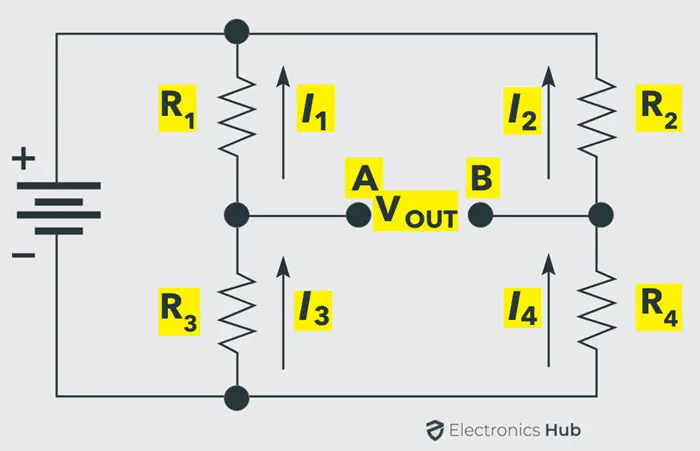
现在,在平衡条件下,电阻 和 之间的电压相等。如果 是 两端的电压, 是 两端的电压,那么:
同样,电阻 (我们称之为 )和 (我们称之为 )之间的电压也相等。因此,
电压比可以表示为:
根据欧姆定律,我们得到:
由于 和 ,我们得到:
从上述方程可以看出,如果我们知道其中三个电阻的值,我们可以轻松计算出第四个电阻的值。
计算电阻的另一种方法
从重新绘制的电路来看,如果 是输入电压,那么 A 点的电压为:
同样,B 点的电压为:
为了使电桥平衡,。但我们知道 。
因此,在平衡电桥条件下,
使用上述方程,我们得到:
对上述方程进行简单变换后,我们得到:
从上述方程可以看出,如果 是未知电阻,其值可以通过已知的 、 和 的值来计算。通常,未知值被称为 ,而在三个已知电阻中,一个电阻(在上述电路中通常是 )通常是一个可调电阻,我们称之为 。
使用平衡惠斯通电桥查找未知电阻
在上述电路中,假设 是未知电阻。因此,我们将其称为 。电阻 和 具有固定值。这意味着 的比值也是固定的。现在,从上述计算来看,为了创建平衡条件,电阻的比值必须相等,即:
由于 的比值是固定的,我们可以轻松调整另一个已知电阻()以实现上述条件。因此,重要的是 是一个可调电阻,我们称之为 。
但是,我们如何检测平衡条件呢?这就是使用检流计(一种老式的安培表)的地方。通过将检流计放置在 A 点和 B 点之间,我们可以检测平衡条件。
将 放入电路中,调整 ,直到检流计指针指向 0。此时,记下 的值。通过以下公式,我们可以计算未知电阻 :
不平衡惠斯通电桥
如果上述电路中的 不等于 0(),则惠斯通电桥被称为不平衡惠斯通电桥。通常,不平衡惠斯通电桥用于测量不同的物理量,如压力、温度、应变等。
要使其工作,传感器必须是电阻式的,即当它所测量的物理量(温度、应变等)发生变化时,传感器的电阻会相应地变化。在前面的电阻计算示例中,我们可以将未知电阻替换为传感器。
使用惠斯通电桥测量温度
现在,让我们看看如何使用不平衡惠斯通电桥来测量温度。我们将在这里使用的传感器称为热敏电阻,这是一种电阻随温度变化的元件。根据热敏电阻的温度系数,温度的变化会使热敏电阻的电阻增加或减少。
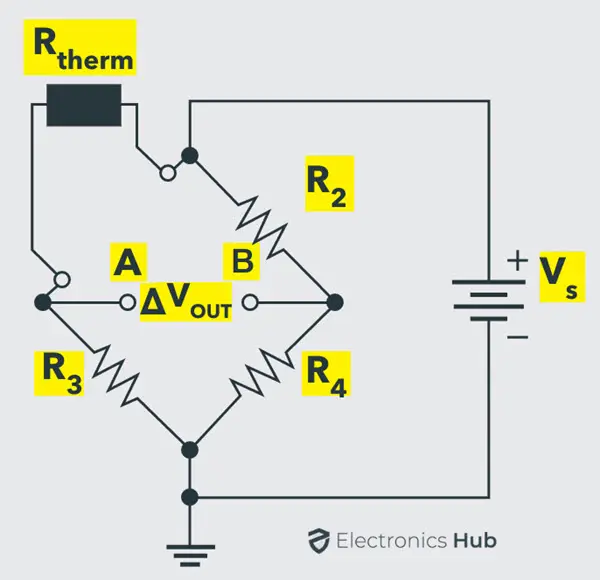
由于这种变化,电桥的输出电压 将成为一个非零值。这意味着电桥的输出电压 与温度成正比。通过校准伏特表,我们可以用输出电压来显示温度。
使用惠斯通电桥测量应变
惠斯通电桥最常用的应用之一是应变测量。应变片是一种其电阻随机械因素(如压力、力或应变)成比例变化的设备。
通常,应变片的电阻范围为 30Ω 至 3000Ω。对于给定的应变,电阻变化可能只是整个范围的一小部分。因此,为了准确测量电阻的微小变化,使用了惠斯通电桥配置。
下图展示了一个惠斯通电桥电路,其中未知电阻被应变片替换。
使用惠斯通电桥测量应变
惠斯通电桥最常用的应用之一是应变测量。应变片是一种其电阻随机械因素(如压力、力或应变)成比例变化的设备。
通常,应变片的电阻范围为 30Ω 至 3000Ω。对于给定的应变,电阻变化可能只是整个范围的一小部分。因此,为了准确测量电阻的微小变��化,使用了惠斯通电桥配置。
下图展示了一个惠斯通电桥电路,其中未知电阻被应变片替换。
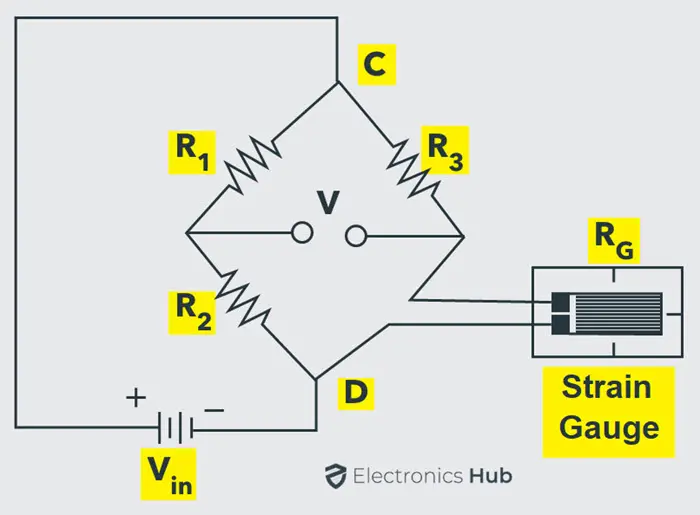
由于外力的作用,应变片的电阻发生变化,从而使电桥失去平衡。输出电压可以校准以显示应变的变化。
应变片和惠斯通电桥的一个常见配置是用于电子秤。在这种情况下,应变片被精心安装为一个称为“称重传感器”的单元,这是一种将机械力转换为电信号的传感器。
通常,电子秤由四个称重传感器组成,其中两个应变片在受到外力时会伸长或拉伸(拉伸型),另外两个应变片在放置负载时会压缩(压缩型)。
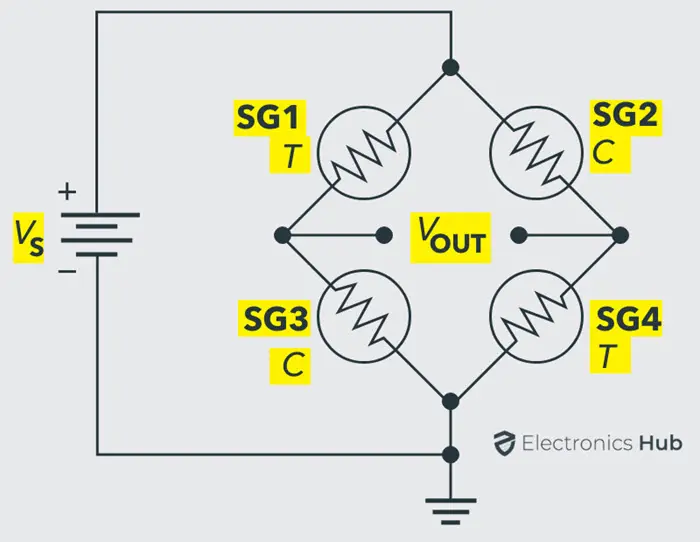
如果应变片被拉伸或压缩,其电阻会增加或减少。因此,这会导致电桥失去平衡。这会在伏特表上产生一个与应变变化相对应的电压指示。如果施加在应变片上的应变越大,伏特表两端的电压差就越大。如果应变为零,则电桥达到平衡,伏特表显示零读数。
这就是使用惠斯通电桥进行精确电阻测量的内容。由于其能够测量电阻的微小变化,惠斯通电桥主要用于应变片和温度计的测量。
应用
- 惠斯通电桥用于精确测量非常低的电阻值。
- 惠斯通电桥与运算放大器结合使用,可用于测量温度、应变、光强等物理参数。
- 通过惠斯通电桥的变体,我们还可以测量电容、电�感和阻抗等量。
总结
本教程是关于惠斯通电桥的入门指南。你已经了解了什么是惠斯通电桥电路、平衡电桥的含义、如何使用惠斯通电桥计算未知电阻,以及不平衡惠斯通电桥如何用于测量温度和应变等不同的物理量。